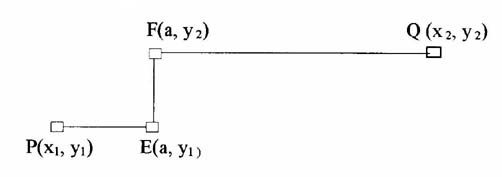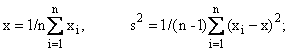АВТОМАТИЗАЦИЯ
УДК 621.3
С. Л. Амбарян
Аналитическая трассировка и ее
применение в задачах
расчета задержек схем
(Представлено академиком А.Т. Кучукяном 18/IX 2000)
При проектировании вычислительной аппаратуры
с использованием печатных плат, программируемых логических ИС (ПЛИС),
многокристальных модулей (МКМ) и т. п. важное значение приобретает задача
расчета задержек (время распространения сигнала) схем, связанная с их конкретной
реализацией [1-5].
Из-за того, что причиной задержки в
значительной мере является длина печатного проводника (проводного монтажа) в
зависимости от технологии изготовления, проектирование современной
вычислительной аппаратуры без учета задержек связей
невозможно.
Задача заключается в том, чтобы были учтены не
только задержки элементов, но и задержки связей (соединений) между ними. Это
предполагает осуществление разрезания, схем, компоновку элементов в
соответствующих конструкциях, размещение элементов в них и наличие результатов
фактической реализации связей трассировка/монтаж. Имея это, а также данные по
расчету задержек элементов, можно приступить к расчету задержек
схемы.
Отметим, что расчет задержек схемы в общем случае
зависит от многих параметров (задержка элемента, длина связи, нагрузка выхода,
наличие обратной связи, конфигурация реализованной цепи и др.), учет которых не
представляет труда. Здесь рассматривается задержка элементов и связей. Будем
предполагать, что каждый элемент типа k имеет определенную задержку типа
tk как общую характеристику для данного
элемента.
В точной постановке задачи можно предположить,
что задержка элемента типа k определяется как время распространения сигнала от
каждого входа xi к определенному выходу yj
| tk(i,j) = tk(xi(k),yj(k)). | |
Задача
компоновки схемы часто решается разработчиками схем, они активно участвуют и при
решении задач размещения. Следует отметить, что решение этих задач в САПР не
представляет большого труда по сравнению с задачей трассировки исходя из
следующих соображений [6]:
- существование приемлемых
решений не вызывает сомнений;
- как правило, решение этих
задач требует меньшего машинного времени, и поэтому их качество можно улучшить
за счет перестановки элементов и итерационных процессов;
-
качество алгоритмов решения этих задач выявляется после этапа трассировки, на
этапе проверки временных параметров.
Таким образом, решение
задач компоновки и размещения можно осуществить за короткий промежуток времени
для достаточно больших схем (узел, устройство). В общем случае при расчете
задержек схем возникает необходимость перекомпоновки и/или переразмещения схемы,
что подчеркивает нецелесообразность потери машинного времени и ресурсов на
решение задач трассировки на данном этапе.
Пусть схема
скомпонована и ее элементы размещены в соответствующие конструктивы, топологии
которых заданы. Если бы удалось все связи реализовать кратчайшими линиями, то
очевидно, что многие проблемы временных параметров схем можно было бы решить до
решения задач трассировки и тем более до фактического изготовления
соответствующих им узлов и устройств. Многие разработчики утверждают, что
временной анализ следует выполнять до завершения топологического проектирования
схем [2,3]. В данной статье предлагается метод расчета временных параметров до
завершения топологического проектирования.
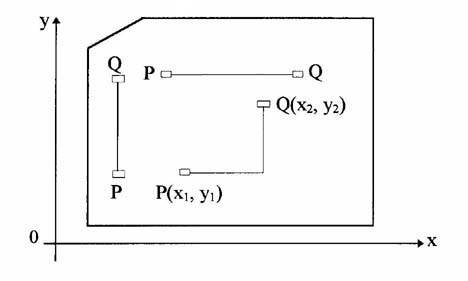
При реализации
связей модулей (ПЛИС, МКМ, печатные платы, узел, устройство - в дальнейшем
модуль) принята их горизонтальная и/или вертикальная реализация - параллельно к
сторонам прямоугольных конструкций этих модулей (см. рис.
1).
Область между двумя параллельными прямыми на
прямоугольной конструкции называется каналом. Прямые,
определяющие канал, называются границами канала. Канал
называется горизонтальным (вертикальным), если его границы
параллельны горизонтальным (вертикальным) сторонам этой конструкции. Прямые
канала, параллельные границам канала, вдоль которых можно провести связь, вместе
с его границами образуют систему магистралей канала.
Максимальное количество магистралей называется пропускной
способностью канала. Реализация связей в таких каналах с помощью его
магистралей называется линейной трассировкой.
|
|
Рис. 1.
Определение 1. Трассировка называется
аналитической, если длина и
трасса проводника между любыми двумя точками данного модуля (контактная
площадка, переходное отверстие, вход/выход) заданы аналитически как определенные
функции от пространственных координат этих точек.
Определение 2.
Аналитическая трассировка называется манхеттеновой, если длина связи задается формулой
|
| L(P,Q) = L(u) = |x2-x1| + |y2-y1| =Δx +
Δy, | |
| Δx = 0,1,2,ј,n, Δy = 0,1,2,ј,
m, | | |
(1) | |
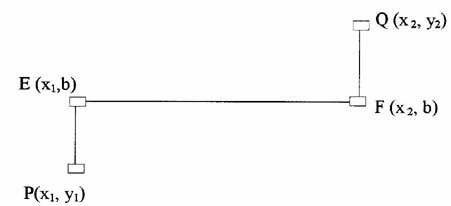
а
трасса проводника задается формулами (см. рис. 2)
| y = b, при x1 Ј x Ј
x2 (2b) | |
Рис. 2.
или (см. рис. 3)
| x = a, при y1 Ј y Ј
y2. (3b) | |
Рис. 3.
Очевидно, что при условии горизонтальной
и/или вертикальной трассировки манхеттеновая трассировка по длине оптимальна
(минимальна)
Манхеттеновая
трассировка - это один из широко распространенных способов линейной
трассировки.
Постановка задачи. Пусть для данной схемы C = C(E,X), где E - элементная база, X - список
цепей, решены классические задачи технического этапа проектирования (разрезание
схем, компоновка и размещение элементов), кроме трассировки/монтажа, согласно
принципам и алгоритмам, функционирующим в инструментальных средствах САПР по
проектированию данного модуля.
Не приступая к решению задач
трассировки, предполагаем, что на данной структуре по всем уровням модулей можно
реализовать манхеттеновую трассировку.
С помощью аналитической трассировки уточняются все вопросы временных
параметров и при необходимости делается повторное разрезание схем, компоновка и
размещение элементов. Только после этого решаются задачи трассировки. На
фактических результатах трассировки выполняется окончательный анализ временных
параметров.
Сказанное сводится к следующим шагам работы
инструментальных средств САПР, включающей в себя подсистему временного
анализа.
1. Определение конструкции
модуля.
2. Разрезание, компоновка
[6].
3. Размещение.
4. Определение
списка электрических соединений.
5. Аналитическая трассировка.
6. Расчет
временых параметров и анализ.
7. Результаты не
удовлетворяют, идти к 4, 3, 2.
8. Фактическая трассировка
и монтаж.
9. Расчет временных параметров и
анализ.
10. Результаты не удовлетворяют, идти к 8, 4, 3,
2.
11. Верификация проекта [7].
12.
Оформление конструкторской документации.
13. Конец.
Во всех шагах данного алгоритма следует понимать либо
решение данной задачи, либо уточнение результатов предыдущих решений. Этот
алгоритм был применен при проектировании печатных плат ТЭЗ ЕС 1170
[8].
Данный метод эффективен в том случае, когда результаты
фактической трассировки близки к принятой аналитической
трассировке. В противном случае необходимо уточнить формулы аналитической
трассировки по фактическим результатам работы алгоритмов трассировки,
функционирующих на данной САПР, проведя статистические исследования на
конструкциях и схемах, подлежащих проектированию. Указанные статистические
исследования алгоритмов трассировки проводятся до работы подсистемы временного
анализа на небольшом количестве экземпляров принятой конструкции и схем,
подлежащих проектированию. Полезными являются также результаты анализа
алгоритмов трассировки на других конструкциях и схемах, ранее проектируемых ими.
Этот метод удобен при использовании технологии монтажа сверхвысокой плотности
(фирма UniStructure), позволяющей изготавливать схемные платы, которые по
плотности компоновки приближаются к микросхемам [5].
Ниже
следует уточнение формул аналитической трассировки на основании указанного выше
статистического исследования.
На прямоугольной конструкции
модуля рассмотрим пару точек P(x1,y1) и
Q(x2,y2), которые необходимо соединить электрической
связью
Пусть
U = {u1,u2, ј,uN} -
множество всевозможных связей на данной конструкции. Каждой связи u сопоставим
некоторую систему функции
| F = {f1(u), f2(u),ј,
fJ(u)}; | |
они в
совокупности оценивают меру трассируемости связи u.
Определение 3.
Две пары связей u и v находятся в
отношении R, eсли имеют место равенства
| fj(u) = fj(v),
для
всех j = 1,2,ј,
J. | |
Отношение
R множество связей разбивает на классы эквивалентности. Рассмотрим два
примера:
a)
J = 1, f1(u) = Δx +
Δy; отношение R
определяется равенством
f1(u) = f1(v).
В этом случае две пары
связей принадлежат одному и тому же классу, если их манхеттеновые расстояния
одинаковы, т. е.
где
Δx + Δy - номер класса (мощность класса - |K| = n + m).
b)
J = 2, f1(u) = Δx, f2(u) =
Δy;
отношение R определяется равенствами
| f1(u) = f1(v), f2(u) = f2(v). | |
В
этом случае две пары связей принадлежат одному и тому же классу, если стороны
прямоугольника связи соответственно равны между собой, т. e.
где Δx Щ
Δy - номер класса(получен
в результате конкатенации(сцепления) значений Δx
и Δy,
мощность класса - |K| = n · m).
Определение 3 может учесть более
тонкие способы разбиения множества связей U на классы эквивалентности, что
способствует выявлению достоинств и недостатков алгоритмов трассировки
применительно к семействам схем и принятой
конструкции.
Пусть для определенного класса k = 1,2,ј,K в результате серии из nk измерений получены
следующие статистические данные:
| L(uk) = Lk + xki; i = 1,2,ј,nk, (5a) | |
где
Lk - манхеттеновая длина связи класса k, 0 Ј xki < Ґ - приращение
связи. Предполагая, что расчетная схема алгоритма не зависит
от индекса k, опустим его.
Пусть для некоторого класса
эквивалентности совокупность по формуле (5а) имеет вид
| L(u) = L° + xi, i = 1,2,ј,
n, (5b) | |
где
L° = Δx +
Δy = const
Вычислим
среднюю длину этих связей
где
Квадрат
среднеквадратического отклонения имеет вид
| s2 = 1/n |
n
е
i=1
|
(xi - x)2. (7) | |
Необходимо
отметить, что не исключен случай, когда статистическая совокупность содержит
значения, превышающие ожидаемые результаты. Такие значения xi в
совокупности можно отнести к "сомнительным значениям" и решить вопрос их
исключения. Упорядочим результаты наблюдения в порядке их возрастания
Предположим,
что "подозрительным" является наибольшее наблюдение. Исключение таких
результатов наблюдений зависит от значения величины
где
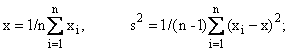
если vn
і
vmax(n,Q), (9)
то значение xn из совокупности исключается, в противном случае
оно остается в составе совокупности, здесь Q = 200 · a, a - уровень значимости
[9].
В результате исключения количество элементов в
совокупности уменьшается на единицу (вновь обозначим n = n - 1), и процесс продолжается до тех пор, пока существует такое
n, для которого имеет место неравенство (9). Для окончательной совокупности,
уточненной описанным способом, вычисляются x и s.
На основе данных совокупности можно
построить функции плотности и распределения вероятностей, при помощи которых
уточняется длина связи.
В частности, после проверки
гипотезы нормальности распределения длин связей в качестве L можно брать
Пусть
x° - оценка абсолютной погрешности
результата, рассмотрим доверительный интервал d
в
который с заданной вероятностью попадает истинное значение приращения длины
связи x.
Величина надежности p (в долях единицы) результата
серии из n і 30 измерений равна [10]:
| p = |
м
п
н
п
о
|
| 0.68269, при x° = 1 · sx, | |
| 0.95450, при x° = 2 · sx, | |
| 0.99730, при x° = 3 · sx, | | |
| |
где
s2x = s2/n.
Использование формул
(11) в отличие от (10) требует наличия генератора псевдослучайных чисел. Выбор
истинного значения x из доверительного интервала d
производится согласно тому, что случайная величина x - абсолютная погрешность
результата серии измерений описывается нормальным законом с дисперсией sx
| y = 1/Ц2psx · exp(-x2/2s2x). | |
Применение
метода аналитической трассировки в ЭВМ ЕС 1170 позволило
аначительно сократить время проектирования и обеспечить временный анализ схем на
ранних этапах разработки.
Ереванский
научно-исследовательский
институт математических машин
Литература
1. Maliniak L. - ED. 1991.
№ 4. P. 45-48, 50.
2. Nass R. - ED. 1989. № 20. P. 31, 32, 37, 38.
3. McLeod J. - EUSA. 1990. № 3. P.
52-54.
4. Milne B. - ED. 1989.
№ 9. P. 71-77.
5. Waller L. - EUSA. 1989. № 8. P. 92, 93.
6. Амбарян С. Л, Мовсесян А.А., Пилипосян Т.Э. - Вопр.
радиоэлектроники. Сер. ЭВТ. 1981. Вып. 16.
7. Амбарян С. Л, Севоян К.С. - Вопр. радиоэлектроники. Сер.
ЭВТ. 1987. Вып. 11.
8. Кучукян А. Т.,
Саркисян Т.Е. - Вопр. радиоэлектроники. Сер. ЭВТ. 1991. Вып.
10.
9. Айвазян С. А. Статистическое исследование зависимостей. М. Металлургия.
1968.
10. Кассандрова О. Н., Лебедев В. В. Обработка результатов наблюдений. М. Наука. 1970.