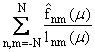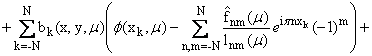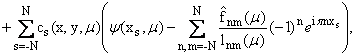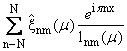ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
УДК 519.62, 519.64
А. Х. Айрапетян
Приближенное символьное решение
задачи Дирихле для
уравнения Гельмгольца
(Представлено академиком А. Б. Нерсесяном
18/XII 2000)
0. Общеизвестно прикладное значение
уравнения Гельмгольца. Упомянем здесь только классические задачи дифракции
электромагнитных волн и задачи, связанные с различными колебательными процессами
в механике сплошных сред. Последние часто возникают в современных прикладных
проблемах механики в связи с взаимoдействиями электромагнитных и упругих полей,
описание которых приводит к системам уравнений Гельмгольца с соответствующими
граничными условиями. В ряде прикладных случаев требуется решить краевую задачу
для уравнения Гельмгольца со свободным параметром. В задаче дифракции, например,
это может быть (см.[1]) волновое число. В таком случае обычные методы решения
приводят к необходимости строить приближенное решение на сети точек в области
изменения параметра с последующей интерполяцией. Это приводит к усложнению
вычислений и связано со значительной потерей времени и точности. Иной путь
применен в работах [2,3] для уравнений с постоянными коэффициентами, зависящими
от параметра. Так, в работе [2] предложен метод получения символьного решения
задач для обыкновенного дифференциального уравнения, а в [3]- для периодического
решения задачи Гурса для гиперболического уравнения. При этом приближенные
решения получаются в виде функциональной суммы, и значения решения можно
восстановить не только в пространственной точке, но и при любом значении
параметра.
В данной работе этот подход применен в случае
следующей граничной задачи Дирихле для уравнения Гельмгольца в квадрате:
|
м
п
п
н
п
п
о |
| L u(x,y,m) є |
¶2 u
¶x2
|
+ |
¶2u
¶y2
|
+ m2 u(x,y) = f(x,y,m),
|x| Ј 1, |y| Ј 1,
| |
| u(x,1,m) = f1(x,m), u(x,-1,m) =
f2(x,m), | |
| u(1,y,m) = y1(y,m), u(-1,y,m) =
y2(y,m), | | |
| |
(0.1) |
где u О
C2([-1,1] × [-1,1] × [a,b]), f1,f2,y1,y2 О C3([-1,1] × [a,b]),
| m О [a,b], m № 0, a,b О
R1. |
1.
Рассмотрим сначала задачу с периодическими граничными условиями
|
м
н
о |
|
|
| u(x,±1,m) = f(x,m), u(±1,y,m) =
y(y,m), f,y О C3([-1,1] × [a,b]). | | |
| |
(1.1) |
Приближенное решение ищется в виде
|
| uN(x,y,m) = |
N
е
k, s=-N
|
aks(x, y,m)f(xk,xs,m) + |
N
е
k=-N
|
bk(x, y,m)f(xk,m) + | |
| + |
N
е
s=-N
|
cs(x, y,m)y(xs,m), | | |
| |
(1.2) |
где xk = [2k/(2N+1)], k = 0,±1,±2,ј,±N, (N
> 0 целое ), а неопределенные коэффициенты a(x,y,m)
= {aks(x,y,m)}Nk,s=-N, b(x,y,m) = {bk(x,y,m)}Nk=-N,
c(x,y,m) = {cs(x,y,m)}Ns=-N
определяются из минимизации следующего функционала (см.[1]) (x,y,m = const, J ® min):
| J = |
N
е
n,m=-N
|
|
RN(eipn x+ ipm y)|2
+ |
N
е
m=-N
|
| RN(
x2 eipm y)|2 + |
N
е
n=-N
|
|
RN(y2eipn
x)|2,
| |
(1.3) |
где
| RN(x,y,m) є
RN(u(x,y,m)) = u(x,y,m) -
uN(x,y,m). | |
(1.4) |
Сведя задачу к соответствующей
линейной системе, после несложных преобразований приходим к представлению
uN(x,y,m) =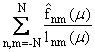 eipn
xe ipm
y+ eipn
xe ipm
y+ |
|
|
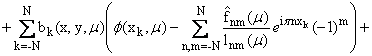
|
(1.5) |
где
lnm(m) =
(ipn)2 + (ipm)2 + m2,
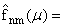 |
1
(2N+1)2
|
|
N
е
k,s =
-N
|
f(xk,xs,m) e-i pnx k e-i pm
xs. | |
Далее
предполагается, что lnm(m) № 0, n, m = 0,±1,±2,ј,±N. Отметим, что
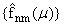 -
двумерное дискретное преобразование Фурье функции f(x,y,m). Коэффициенты { bk(x,y,m) } , { cs(x,y,m) }
определятся из следующей системы:
-
двумерное дискретное преобразование Фурье функции f(x,y,m). Коэффициенты { bk(x,y,m) } , { cs(x,y,m) }
определятся из следующей системы:
|
м
п
п
н
п
п
о |
|
N
е
k=-N
|
bk(x,y,m)gm(xk,1,m) + |
N
е
s=-N
|
ck(x,y,m)gm(1,xs,m) = gm(x,y,m), | |
|
N
е
k=-N
|
bk(x,y,m)gn(1,xk,m) + |
N
е
s=-N
|
ck(x,y,m)gn(xs,1,m) = gn(y,x,m), | | |
| |
(1.6) |
где
gm(x,y,m) = eipm
y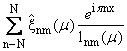 -
x2eipm
y, m,n = 0,±1,±2,ј,±N. -
x2eipm
y, m,n = 0,±1,±2,ј,±N. |
|
Задачу
(0.1) общего вида можно свести к задаче (1.1), сделав, например, замену
переменных
|
| v(x,y,m) = u(x,y,m) + |
y2(y,m)(x - 1)
2
|
- |
y1(y,m)(x + 1)
2
|
, | |
|
|
| w(x,y,m) = v(x,y,m) + |
v(x, -1,m)(y - 1)
2
|
- |
v(x, -1,m)(y + 1)
2
|
. | | |
| |
(1.7) |
Tогда для функции w(x,y,m) получится эквивалентная задача (1.1), но уже с нулевыми граничными условиями (в (1.1) f(x,m) є 0, y(y,m) є
0).
Приближенное решение задачи (1.1) при таком подходе
оказывается интерполяционным. Именно, для любой гладкой функции f(x,y,m) соотношение (1.1) удовлетворяется для (1.2) на сети (x,y)
О {(xk,xs)}, а в граничных точках
u(xk,1,m) = f(xk), u(1,xs,m) = y(xs,m), k,s = 0,±1,±2,ј,±N.
Оказывается, что применением свойств циркулянта,
содержащегося в (4N + 2) × (4N + 2) - матрице системы (1.6), последнюю можно свести к
систeме с (2N + 1) × (2N + 1) - матрицей.
В случае однородной
задачи (0.1) ( f(x,y,m) є 0 )
замена u ® w неизвестной функции (1.7) позволяет
существенно упростить алгоритм.
2. Предложенная
схема апробовaна в многочисленных экспериментах. При фиксированном значении
параметра m = m0
для соответствующих ошибок приняты следующие обозначения:
| er1(n) = |
||RN(x,y,m0)||L2
||uN(x,y,m0) ||L2
|
, er2(n) = |
|
, |x| Ј 1 ,|y| Ј 1,
| |
(2.1) |
а при фиксированном значении
переменной y = y0 - обозначения
| er3(n) = |
||RN(x,y0 ,m)||L2
||uN(x,y0,m) ||L2
|
, er4(n) = |
|
, |x| Ј 1,1 Ј m Ј
3, | |
(2.2) |
где N = 2n, n =
1,2,...5 . Таким образом, в экспериментах количество точек сети {xk}
менялось от 5 до 65. Приведенные здесь численные результаты относятся к
следующим задачам.
Рис.
1. Рис.
2.
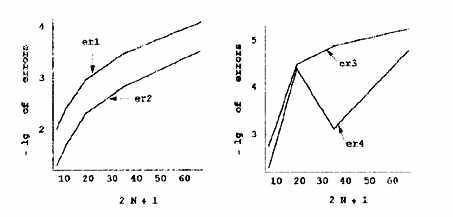
Рис. 1. Десятичные логарифмы обратных
величин равномерных и L2-ошибок RN(x,y,m0) задачи 1 при m0 = 1 и различных значениях N.
Рис. 2. Десятичные логарифмы обратных
величин равномерных и L2-ошибок RN(x,y0,m) задачи 1 при y0=0.1, |x| Ј
1, 1 Ј m Ј 3 и различных значениях N.
Задача 1. Функцию
u(x,y,m) =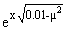 sin(0.1y)
-
sin(0.1y)
-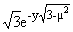 cos(
cos(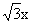 ) считаем точным решением однородной задачи (1.1) (f(x,y,m) = 0) при соответствующих граничных условиях общего вида.
Отметим, что приближенное решение в этом случае имеет символьный вид, зависящий
как от x, y, так и от m. Рис. 1,2 характеризуют
результаты решения задачи 1.
) считаем точным решением однородной задачи (1.1) (f(x,y,m) = 0) при соответствующих граничных условиях общего вида.
Отметим, что приближенное решение в этом случае имеет символьный вид, зависящий
как от x, y, так и от m. Рис. 1,2 характеризуют
результаты решения задачи 1.
Рис.
3. Рис.
4.
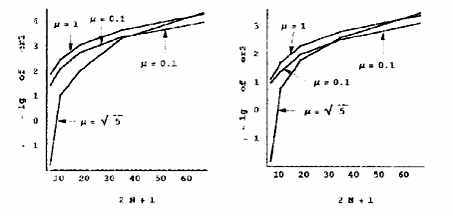
Рис. 3. Десятичные логарифмы
обратных величин L2-ошибок RN(x,y,m0) задачи 2 при различных значениях N и m0.
Рис. 4. Десятичные логарифмы обратных величин равномерных
ошибок RN (x,y,m0) задачи 2 при
различных значениях N и m0.
Задача 2. Функцию u(x,y,m) = [(sin(2xm + 1.4y -1))/(2 + cos(xy -1))] считаем
точным решением задачи (0.1) при соответствующей правой части f(x,y,m) и граничных условиях. Решение в этом случае имеет
символьный вид, зависящий только от (x ,y), а различие в способах представления
решений задач 1 и 2 обусловлено тем, что численные эксперименты проведены для
дискретных точек параметра m. Такое ограничение
наложено из-за недостаточности оперативной памяти применяемого компьютeра. Рис.
3, 4 характеризуют результаты решения задачи
2.
3. На основе приведенных результатов можно
сделать следующие выводы. Как видно из рис. 1 - 4, описанный алгоритм по
L2-норме имеет примерный порядок O([1/(N2)]) (N
® Ґ). Это подтверждается и в
других экспериментах. На рис. 2 эффект падения точности при N = 33
объясняется ситуацией вблизи границы, а на рис. 3, 4 видно, что при
увеличении значения параметра точность алгоритма возрастает. При данном подходе
приближенное решение представляется явной формулой, содержащей параметр, что
позволяет эффективным образом исследовать приближенное символьное решение при
различных вариациях переменных, как это видно из рис. 1, 2. Возможны
решения различных задач минимизации по параметру m.
Tочность порядка 10-3 - 10-7,
продемонстрированная на рис. 1-4, достаточна для многих приложений.
Вычисления проведены на PC Pentium I, 16 RAM, 100 Mz. Разумеется, с ростом
производительности применяемого компьютера, при одновременном увеличении
оперативной памяти, предложенный алгоритм будет работать быстрее и точнее.
Вычисления проведены посредством системы MATHEMATICA 3.0[4].
Институт математики НАН РА
Литература
1. Лебедев Н.Н. Специальные
функции и их приложения. М-Л. Физматгиз. 1963. 358 с.
2.
Нерсесян А.Б., Погосян А.В., Саакян К.П. - ДНАН
Армении. 1998. Т. 98. № 2. С. 96-101.
3. Саакян К.П. Параметрическая интерполяция и приближенное
нахождение периодических решениий интегро-дифференциально-разностных уравнений.
Канд. дис. Ин-т проблем информатики и автоматизации НАН РА. Ереван.
1999.
4. Stephan Wolfram. The
Mathematica Book.Third Edition,Wolfram Media,1996
![]() -
двумерное дискретное преобразование Фурье функции f(x,y,m). Коэффициенты { bk(x,y,m) } , { cs(x,y,m) }
определятся из следующей системы:
-
двумерное дискретное преобразование Фурье функции f(x,y,m). Коэффициенты { bk(x,y,m) } , { cs(x,y,m) }
определятся из следующей системы: ![]() sin(0.1y)
-
sin(0.1y)
-![]() cos(
cos(![]() ) считаем точным решением однородной задачи (1.1) (f(x,y,m) = 0) при соответствующих граничных условиях общего вида.
Отметим, что приближенное решение в этом случае имеет символьный вид, зависящий
как от x, y, так и от m. Рис. 1,2 характеризуют
результаты решения задачи 1.
) считаем точным решением однородной задачи (1.1) (f(x,y,m) = 0) при соответствующих граничных условиях общего вида.
Отметим, что приближенное решение в этом случае имеет символьный вид, зависящий
как от x, y, так и от m. Рис. 1,2 характеризуют
результаты решения задачи 1.