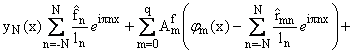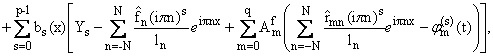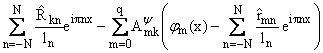ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
УДК 519.62, 519.64
А. В. Погосян
О сходимости приближенного символьного
решения
дифференциальных уравнений
((Представлено академиком А.Б. Нерсесяном 30/XI 2000)
В [1,2] предложена схема параметрической
интерполяции, позволяющая строить обширный класс новых аппроксимационных формул
и обобщать уже известные. При таком подходе выбор параметров предоставляет
возможность адаптироваться к конкретным задачам.
Такая
схема успешно реализована в [2-4] для получения символьных приближенных решений
операторных уравнений типа свертки на отрезке вида Lu = f, для которых
| L(ei lx) = l(l)eilx, l
О | C, x О [-1,1]. | |
(0.1) |
Здесь эта схема
использована для получения численного решения подобных операторных уравнений в
виде полиномиально-тригонометрической интерполяции (ПТИ). Полученные формулы
обобщают и усиливают результаты работы [4]. Изучается эффект Фурье - Бернулли
(ФБ-эффект), впервые обнаруженный в [8] для ПТИ гладких функций (см. также
[5-7]). Его суть состоит в ускоренной сходимости внутри области интерполяции (по
сравнению с интерполяциями, где используются точные значения производных), когда
скачки интерполируемой функции вычисляются приближенно, несмотря на то, что
последние почти всегда чувствительно отличаются от
точных.
Характер сходимости изучен на основе серии
численных экспериментов, выполненных посредством системы MATHEMATICA 3.0 [9].
1. Рассмотрим задачу Коши
|
| Ly(x) := |
p
е
n=0
|
qn |
dn y
dxn
|
= f(x), x О [-1,1], | |
| y(n)(t) = Yn, n = 0,ј,p-1, | | |
| |
(1.1) |
где qn (n = 0,ј,p) от x не зависят, t О [-1,1] - фиксированное число. Хорошо известно, что задача
(1.1) корректна в Cp[-1,1] (f
О Cp).
Решение ищем в
виде
| yN(x) := |
N
е
k=-N
|
ak(x)f(xk) + |
p-1
е
k=0
|
bk(x)Yk, | |
(1.2) |
где xk = [2 k/( 2N+1)],
k = 0,±1,ј,±N (N і 1-целое). Для нахождения
коэффициентов
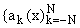 и
и
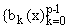 потребуем, чтобы формула (1.2) была точной для систем { ei pn x}, n = -N + q2,ј,N - q1 (q2 = q1 = [(q + 1) / 2], при
нечетных q и q1 = [q / 2] + 1, q2 = [q / 2], при четных q, q і 0-целое),
потребуем, чтобы формула (1.2) была точной для систем { ei pn x}, n = -N + q2,ј,N - q1 (q2 = q1 = [(q + 1) / 2], при
нечетных q и q1 = [q / 2] + 1, q2 = [q / 2], при четных q, q і 0-целое),
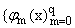 и
и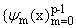 . Будем считать, что объединенная система функций
{eipn x,jm(x),ym(x)}
линейно независима на [-1,1].
. Будем считать, что объединенная система функций
{eipn x,jm(x),ym(x)}
линейно независима на [-1,1].
После несложных преобразований придем к формуле
|
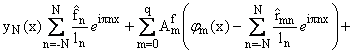
|
(1.3) |
где
введены следующие обозначения:
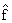 n= n= |
1
2N + 1
|
|
N
е
k=-N
|
f(xk)e-ipn
xk, |n| Ј
N, | |
| ln = |
L(eipn
x)
eipn x
|
, |n| Ј N, | |
|
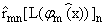 , |n| Ј N; m = 0,ј,q, , |n| Ј N; m = 0,ј,q, | |
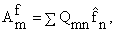 m = 0,ј,q,
m = 0,ј,q, |
|
Qmn
- элементы матрицы, обратной к матрице ||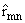 ||, (m = 0,ј,q; n = -N,ј, -N + q2 - 1, N - q1 + 1, ј, N), а под
символом е понимаем суммирование по значениям n = -N,ј, -N + q2 + 1,N - q1 + 1, ј, N.
||, (m = 0,ј,q; n = -N,ј, -N + q2 - 1, N - q1 + 1, ј, N), а под
символом е понимаем суммирование по значениям n = -N,ј, -N + q2 + 1,N - q1 + 1, ј, N.
Функции bk(x) в (1.3)
определяются из следующей системы:
|
p-1
е
s=0
|
Mksbs(x) = Fk(x), k = 0,ј,p - 1, | |
(1.4) |
где
Fk(x) = yk(x) -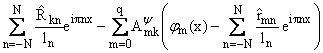 , k = 0, ј, p - 1. , k = 0, ј, p - 1. |
|
| Mks = Fk(s)(t), k = 0,ј,p - 1; s = 0,ј,p - 1, | |
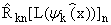 , |n| Ј N; k = 0,ј,p - 1, , |n| Ј N; k = 0,ј,p - 1, | |
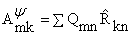 , m = 0, ј, q; k = 0,ј,p - 1. , m = 0, ј, q; k = 0,ј,p - 1. | |
Алгоритм
(1.3)-(1.4) назовем алгоритмом A.
Как следует из
результатов работ [5,6], величины
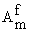 и
и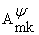 являются приближенными
значениями чисел
являются приближенными
значениями чисел
|
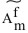
|
= |
q
е
k=0
|
(f(k)(1) - f(k)(-1))Pkm, m = 0, ј, q, | |
|
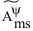
|
= |
q
е
k=0
|
(Rs(k)(1) - Rs(k)(-1))Pkm, m = 0,ј,q; s = 1, ј, p, | |
где
Rm(x) = L(ym(x)), а Pkm
- элементы матрицы, обратной к матрице [rm(k)(1) - rm(k)(-1)]
(k = 0,ј,q; m = 0,ј,q;
rm(x) = L(jm(x))).
Замечание 1. Если в соотношениях
(1.3)-(1.4) формально заменить числа
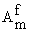 и
и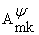 нулями, то получатся формулы
работы [3].
нулями, то получатся формулы
работы [3].
Замечание 2. Метод Бернулли
(см. [5,6]) также содержится в (1.3)-(1.4) при L є I (I
- единичный оператор), p = 0 и jm(x) = Bm(x) (Bm(x) -
полиномы Бернулли), при этом все суммы вида 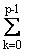 надо
считать равными нулю.
надо
считать равными нулю.
Алгоритмом B назовем действия
алгоритма A, в котором
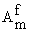 заменены через
заменены через
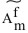 . Алгоритмом C назовем действия
алгоритма A, в котором и
. Алгоритмом C назовем действия
алгоритма A, в котором и
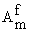 и
и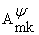 заменены соответственно
числами
заменены соответственно
числами 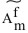 и
и
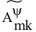 . Алгоритмы B и C изучены в
работе [4].
. Алгоритмы B и C изучены в
работе [4].
Замечание 3. Соответствующие
алгоритмы можно получить, если в алгоритмах A, B и C все
дискретные преобразования Фурье заменить соответствующими коэффициентами Фурье
(см. [8]). Здесь их свойства не изучаются.
2.Чтобы продемонстрировать ФБ-эффект
(ускоренную сходимость) в алгоритмах A, B и
C, рассмотрим задачу, решением которой является функция e(a+ib)x, зависящая от двух
параметров a и b
|
| y(6) + ay(5) + by = ((a + ib)6 + a(a + ib)5 + b)e(a+i
b)x, x О [-1,1], | |
| y(s)(0) = (a + i b)s, s = 0, .ј, 5. | | |
| |
(2.1) |
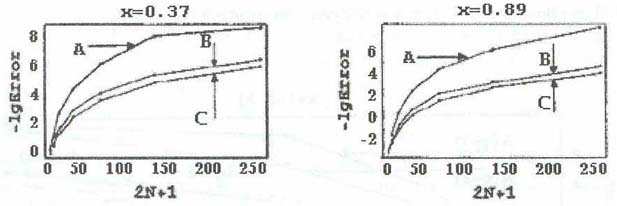
На рис. 1
представлены десятичные логарифмы обратных величин абсолютных ошибок после
применения алгоритмов A, B и C для примера 2.1, при
фиксированных значениях x = 0.37 (слева) и при x = 0.89 (справа), когда a О [2,3], b О [4,9], q = 1. Здесь jm(x) = Bm(x), m = 1, .ј, q + 1,
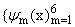 = {ex,e-x,e2 x,e-2
x,e3 x,e-3 x}.
= {ex,e-x,e2 x,e-2
x,e3 x,e-3 x}.
Рис. 1. Логарифмы обратных величин
абсолютных ошибок после применения
алгоритмов A, B и C для примера
2.1, при фиксированных значениях x = 0.37 (слева)
и при x = 0.89 (справа),
когда a О [2,3], b О [4,9], q = 1.
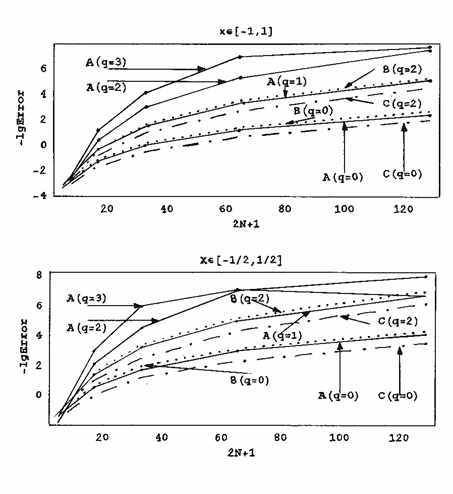
На рис. 2 представлены десятичные логарифмы обратных
величин абсолютных ошибок после применения алгоритмов A, B и
C для примера 2.1, при различных значениях q, когда a О [2,3], b = a2, x О [-1,1] (наверху) и x О [-1/2,1/2] (внизу). Функции jm(x) и ym(x)
выбраны, как и на рис 1.
На основании этих результатов и
многочисленных других экспериментов можно сделать следующее
заключение:
Хорошо известны трудности, возникаюшие при
численном решении уравнений, когда решение, коэффициенты или правая часть
уравнения зависят от нескольких параметров. В частности, это приводит к резкому
повышению сложности соответствующих алгоритмов, поскольку вычисления необходимо
осуществлять на достаточно густой дискретной сети параметров. Алгоритмы
A, B и C позволяют решать такие задачи посредством одного
символьного разложения. При этом алгоритм A намного эффективнее двух
других, как это видно, в частности, на рисунках 1 и
2.
Такие алгоритмы можно получить также и при решении
начальных задач более общего вида, и в частности - для интегро-дифференциальных
уравнении определенного сверточного типа, для нахождения периодических решений
уравнений с запаздыванием (см. [3,4]), а также при решении соответствующих
граничных задач (см. [1]).
Алгоритм C неустойчив
при переходах от четных q к нечетным. Точность при этом, для данного N, почти не
увеличивается и на всем отрезке [-1,1] и на его части
[-1/2,1/2]. В этом смысле алгоритм B также
неустойчив. На рисунке 2 алгоритмы B и C при q = 1 и q = 3 не
представлены, так как они практически не отличаются от соответствуюших
алгоритмов при q = 0 и q = 2. О такой неустойчивости отмечено в [4], а также в [6],
при решении уравнений в частных производных. У алгоритма A нет такой
неустойчивости. Например, для 2N + 1 = 129 при переходе от q = 0 к q = 1 (см. рис. 2),
точность увеличилась в 500 раз на отрезке [-1,1] и в
100 раз - на отрезке [-1/2,1/2].
Рис. 2. Логарифмы обратных величин
абсолютных ошибок после применения
алгоритмов A, B и C для примера
2.1, для различных значений q и N, когда a
О [2,3],
b = a2 x О
[-1,1] (наверху) и x О [-1/2,1/2]
(внизу).
При решении дифференциальных уравнений ФБ-эффект
усиливается, по сравнению с интерполяцией функции, в том смысле, что он
распространяется на весь отрезок [-1,1]. О
существовании ФБ-эффекта в алгоритмах A, B и C на отрезках
[-1,1] и [-1/2,1/2]
свидетельствует тот факт, что алгоритм A, - для данного N и q, - дает
существенно лучшую точность, чем алгоритмы B и C, несмотря на то,
что он использует приближенные значения скачков правой части, которые
значительно отличаются от точных значений. Аналогичное преимущество имеет
алгоритм B по отношению к C.
На отрезке
[-1/2,1/2] алгоритм C уступает по точности
алгоритмам B и A почти для всех q и N. Например, при q = 0 и
2N + 1 = 129 (рис. 2) - в 6 и 3 раза, при q = 1 и 2N + 1 = 129 - в 3 и 500 раз, a при q = 2
и 2N + 1 = 129 - в 7 и 70 раз соответственно. Аналогичное отставание по точности и у
алгоритма C на отрезке [-1,1]. Например (рис.
2), при q = 0 и 2N + 1 = 129 алгоритм C уступает по точности алгоритмам
B и A на [-1,1] в 4-5 раз, a при q = 1 и 2N + 1 = 129 - в 2 и 3000 раз
соответственно.
При q = 0 точность алгоритмов A и
B, как правило, примерно одинакова. Однако ситуация меняется при q і 1, когда алгоритм B уступает по точности алгоритму
A, а в некоторых случаях - на несколько порядков.
Из рис. 1 и 2 хорошо видно, что при q і 3 уже
накапливаются ошибки округления. Этого можно частично избежать: либо
соответствующим выбором функций jm(x) и
ym(x), либо нахождением скачков производных
правой части одним из способов, предложенных в [5-8].
Институт математики НАН РА
Литература
1. Nersessian A.B. In:
Collection of Works Dedicated to the Memory of Mkhitar M. Djrbashian. Yerevan,
Louys, 1995. P. 133-138.
2. Нерсесян А.Б. -
ДНАН Армении. 1998. Т. 98. № 1. С. 23-29.
3.
Нерсесян А.Б., Погосян А.В., Саакян К.П. - ДНАН
Армении. 1998. Т. 98. № 2. С. 96-101.
4. Айрапетян А.Х., Нерсесян А.Б. Депонировано в АрмНИИНТИ
09.03.00, N22-Ар00.
5. Knut S. Eckhoff. -
Mathematics of Computation. 1998. V. 67, N223, July. P.
1063-1087.
6. Eckhoff K.S., Wasberg C.E. On the numerical approximation of derivatives by a modified
Fourier collocation method, Thesis of Carl Erik Wasberg. Department of
Mathematics. University of Bergen. Norway. 1996.
7. Gelb A., Gottlieb D. - Computers Math. Applic. 1997. V.
33. N11. P. 35-58.
8. Нерсесян А.Б., Погосян
А.В. Депонировано в АрмНИИНТИ 07.07.00,
N45-Ар00.
9. Wolfram S. The
MATHEMATICA book, Third Edition, Wolfram Media, Cambridge University Press.
1996.
![]() и
и
![]() потребуем, чтобы формула (1.2) была точной для систем { ei pn x}, n = -N + q2,ј,N - q1 (q2 = q1 = [(q + 1) / 2], при
нечетных q и q1 = [q / 2] + 1, q2 = [q / 2], при четных q, q і 0-целое),
потребуем, чтобы формула (1.2) была точной для систем { ei pn x}, n = -N + q2,ј,N - q1 (q2 = q1 = [(q + 1) / 2], при
нечетных q и q1 = [q / 2] + 1, q2 = [q / 2], при четных q, q і 0-целое),
![]() и
и![]() . Будем считать, что объединенная система функций
{eipn x,jm(x),ym(x)}
линейно независима на [-1,1].
. Будем считать, что объединенная система функций
{eipn x,jm(x),ym(x)}
линейно независима на [-1,1].
![]() ||, (m = 0,ј,q; n = -N,ј, -N + q2 - 1, N - q1 + 1, ј, N), а под
символом е понимаем суммирование по значениям n = -N,ј, -N + q2 + 1,N - q1 + 1, ј, N.
||, (m = 0,ј,q; n = -N,ј, -N + q2 - 1, N - q1 + 1, ј, N), а под
символом е понимаем суммирование по значениям n = -N,ј, -N + q2 + 1,N - q1 + 1, ј, N.![]() и
и![]() являются приближенными
значениями чисел
являются приближенными
значениями чисел ![]() и
и![]() нулями, то получатся формулы
работы [3].
нулями, то получатся формулы
работы [3].
![]() надо
считать равными нулю.
надо
считать равными нулю.![]() заменены через
заменены через
![]() . Алгоритмом C назовем действия
алгоритма A, в котором и
. Алгоритмом C назовем действия
алгоритма A, в котором и
![]() и
и![]() заменены соответственно
числами
заменены соответственно
числами ![]() и
и
![]() . Алгоритмы B и C изучены в
работе [4].
. Алгоритмы B и C изучены в
работе [4].
![]() = {ex,e-x,e2 x,e-2
x,e3 x,e-3 x}.
= {ex,e-x,e2 x,e-2
x,e3 x,e-3 x}.