МАТЕМАТИКА
УДК 519.68:510
С. А. Нигиян, С. А. Аветисян
О решениях рекурсивных уравнений с
отделяющейся
переменной в бестиповом
(Представлено академиком Н.У.
Аракеляном 30/XI 2000)
1. Используемые определения и
результаты (см.[1]). Зафиксируем счетное множество
переменных V. Множество термов L является наименьшим
множеством, удовлетворяющим следующим условиям: 1) если x О V, то x О L; 2) если t1,t2 О L, то (t1t2)
О L; 3) если x О V и t О L, то (lx.t) О L.
Введем
сокращенную запись термов: терм (ј (t1t2) .јtk), где ti О
L, i = 1, .ј, k,
k > 1, условимся обозначать t1t2 ј tk; терм (lx1(lx2(ј (lxm.t)ј), где xj О V, t О L, условимся обозначать lx1x2 ј xm.t, j = 1,ј,m, m
> 0.
Традиционным образом вводятся понятия свободного и
связанного вхождения переменной в терм, понятие свободной переменной терма.
Множество всех свободных переменных терма t условимся обозначать FV(t). Терм, не
содержащий свободных переменных, назовем замкнутым. Множество всех замкнутых
термов будем обозначать L0.
Через t[x] условимся
обозначать терм t с указанием интересующей нас переменной x. Через t[tў] обозначим терм, полученный в результате одновременной
подстановки терма tў в терм t вместо всех свободных
вхождений переменной x. Через t{x, ј ,x} условимся
обозначать терм t с указанием всех k і 0 свободных
вхождений переменной x (слева направо). Через t{t1, ј , tk} обозначим терм, полученный в результате
одновременной подстановки термов t1,ј,tk в терм t вместо соответственно первого,
второго и т. д., k-го свободных вхождений переменной
x.
Подстановку назовем допустимой, если ни одна свободная
переменная подставляемого терма не связывается в результате подстановки. Мы
будем рассматривать только допустимые подстановки.
Термы
t1 и t2 назовем конгруэнтными (обозначим t1
є t2), если один терм можно получить из
другого переименованием связанных переменных. Далее мы не будем отличать
конгруэнтные термы.
Напомним понятие b-редукции:
| b = {(lx.t[x])tў, t[tў]) | t,tў О L, x О
V}. | |
Одношаговая
b-редукция (®b), b-редукция (®®b) и b-равенство (=b) определяются обычным образом. Далее условимся
отношение ®b
обозначать ®, отношение ®®b обозначать ®®, отношение =b обозначать =, т. е. опуская символ b.
Напомним, что терм (lx.t[x])tў называется b-редексом (далее просто редексом). Терм, не содержащий
редексов, называется b-нормальной формой (далее просто
нормальной формой). Множество всех нормальных форм условимся обозначать NF.
Множество всех замкнутых нормальных форм - NF0. Будем говорить, что
терм t имеет нормальную форму, если существует такой терм t О NF, что t = tў.
Напомним теорему о неподвижной точке,
которая гласит о том, что для всякого терма t О L имеет место следующее:
где Y є lh.(lx.h(xx))(lx.h(xx)) - конструктор
неподвижной точки, x,h О V. Мы будем
широко использовать следствие теоремы Чёрча - Россера (CR-теоремы),
утверждающее, что для любого терма t О L имеют место следующие два утверждения:
|
| t = tў, tў О
NF Ю t ®® tў, | |
| t = tў, t = tўў, tў, tўў О NF Ю tў
є tўў. | | |
| |
Мы
также будем использовать теорему о замене для b-равенства, которая состоит в следующем: пусть tt1 есть терм с фиксированным вхождением
подтерма t1, а tt2 - терм, полученный из терма tt1 в результате замены фиксированного
вхождения подтерма t1 на терм t2, тогда t1 = t2 Ю tt1 = tt2.
2. Уравнения с отделяющейся переменной и свойства их решений. Рассмотрим уравнение
где f О V, t[f] О L, FV(t[f]) М {f}.
Рассмотрим решение t уравнения (1)
Теорема 1.
Пусть дано уравнение (1) и его решение (2),
пусть термы t0,n1,n2,ј,nk О NF0, где
k і 0, тогда
| tn1n2јnk ®® t0 Ы $n і 1, tn[f]n1n2јnk ®® t0,
| |
где t0[f] є f, tm[f] є t[tm-1[f]],
m і 1.
Перед тем как перейти к непосредственному доказательству теоремы 1,
введем одно понятие и докажем лемму 1.
Пусть t[f] О L, f О V, FV(t[f]) = {f} и не существует такого
tў О L0, что t[f] ®® tў. Всякий терм вида (lx.t1[xx])(lx.t2 [xx]), где x О V,
t1,t2 О L, t[f] ®® t1[f], t[f] ®® t2 [f], назовем ядром.
Одношаговую редукцию назовем ядерной, если её редексом является
ядро.
Лемма 1. Пусть t[f] О L, f О V, FV(t[f]) = {f} и не существует такого
tў О L0, что t[f] ®® tў.
Пусть
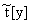 О L, y О V,
О L, y О V, 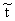 [(lx.t[xx])(lx.t[xx])] ®® t0, где t0
О NF0 и число ядерных редукций равно r і 0. Тогда
[(lx.t[xx])(lx.t[xx])] ®® t0, где t0
О NF0 и число ядерных редукций равно r і 0. Тогда
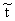 [tn[f]] ®® t0, если n і r.
[tn[f]] ®® t0, если n і r.
Доказательство леммы следует из утверждения 1.
Утверждение 1.
Пусть t[f] О L, f О V,
FV(t[f]) = {f} и не существует такого tў О L0, что t[f] ®® tў.
Пусть
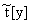 О L, y О V и
О L, y О V и
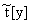 є
є
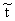 {y, ј , y},
где число свободных вхождений
переменной y в терм
{y, ј , y},
где число свободных вхождений
переменной y в терм
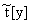 равно k і
0.
равно k і
0.
Пусть ti[f], tiў[f] О L, t[f] ®® ti [f], t[f] ®® tiў[f], i = 1, ј , k, и
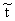 {(lx.t1[xx])(lx.t1ў[xx]), ј , (lx.tk[xx])(lx.tkў[xx])} ®® t0, где t0
О NF0 и число ядерных редукций, редексы
которых получены в процессе редукции из подставленных в терм
{(lx.t1[xx])(lx.t1ў[xx]), ј , (lx.tk[xx])(lx.tkў[xx])} ®® t0, где t0
О NF0 и число ядерных редукций, редексы
которых получены в процессе редукции из подставленных в терм
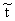 {y, ј , y} ядер, равно r і
0.
{y, ј , y} ядер, равно r і
0.
Тогда
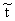 {tn1[f], ј , tnk[f]} ®® t0, если ni
і r, i = 1, ј , k.
{tn1[f], ј , tnk[f]} ®® t0, если ni
і r, i = 1, ј , k.
Доказательство. Пусть r = 0, тогда очевидно, что
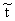 {tn1
[f], ј , tnk[f]} ®® t0. Пусть r > 0 и
утверждение 1 верно для r - 1. Докажем для r. Легко
видеть, что имеет место следующее:
{tn1
[f], ј , tnk[f]} ®® t0. Пусть r > 0 и
утверждение 1 верно для r - 1. Докажем для r. Легко
видеть, что имеет место следующее:
|
|
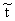 {(lx.t1[xx])(lx.t1ў[xx]),ј,(lx.tk[xx])(lx. tkў[xx])} ®® {(lx.t1[xx])(lx.t1ў[xx]),ј,(lx.tk[xx])(lx. tkў[xx])} ®® | |
|
_
t¢1
|
{(lx . |
_
t¢1
|
[xx])(lx . |
_
t¢1
|
[xx]), ј , (lx . |
_
ti
|
[xx])(lx . |
_
t¢
|
[xx]),ј,(lx . |
_
ts
|
[xx])(lx . |
_
t¢s
|
[xx])}, | | |
| |
где
(lx .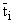 [xx])(lx .
[xx])(lx .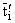 [xx]), i = 1, ј , s, s і 1, есть все ядра,
полученные в процессе редукции из ядер, подставленных в терм
[xx]), i = 1, ј , s, s і 1, есть все ядра,
полученные в процессе редукции из ядер, подставленных в терм
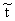 {y,ј,y}, и число ядерных редукций, редексами которых являются
такие ядра, равно 0. Далее мы фиксируем момент первой интересующей нас ядерной
редукции:
{y,ј,y}, и число ядерных редукций, редексами которых являются
такие ядра, равно 0. Далее мы фиксируем момент первой интересующей нас ядерной
редукции:
|
|
~
t¢1
|
{(lx . |
_
t1
|
[xx])(lx . |
_
t¢1
|
[xx]), ј , (lx . |
_
ti
|
[xx])(lx . |
_
t¢i
|
[xx]), ј , (lx . |
_
ts
|
[xx])(lx . |
_
t¢s
|
[xx])}® | |
|
~
t¢1
|
{(lx . |
_
t1
|
[xx])(lx . |
_
t¢1
|
[xx]), ј , |
_
ti
|
[(lx . |
_
t¢i
|
[xx])(lx . |
_
t¢i
|
[xx])], ј , (lx . |
_
ts
|
[xx])(lx . |
_
t¢s
|
[xx])}
є | |
|
~
t1
|
{(lx . |
_
t1
|
[xx])(lx . |
_
t¢1
|
[xx]), ј , (lx . |
_
t¢i
|
[xx])(lx . |
_
t¢i
|
[xx]), ј , (lx . |
_
t¢i
|
[xx])(lx . |
_
t¢i
|
[xx]),ј | | |
| |
ј , (lx .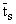 [xx])(lx .
[xx])(lx .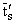 [xx])} ®® (число ядерных редукций, редексы
которых получены в процессе редукции из подставленных в терм
[xx])} ®® (число ядерных редукций, редексы
которых получены в процессе редукции из подставленных в терм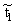 ядер, равно r - 1) ®® t0.
ядер, равно r - 1) ®® t0.
С другой стороны:
|
~
t
|
{ tn1[f], ј , tnk[f]} ®® |
~
t¢1
|
{
tn1ў[f],ј,tniў[f], ј ,
tnsў[f]} ,
| |
где nўi О { n1,ј, nk} , i = 1,ј,s, s і 1. Далее имеем:
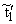 { tnў1[f],ј,tnўi[f],ј,tnўs[f]} ®®
{ tnў1[f],ј,tnўi[f],ј,tnўs[f]} ®®
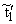 {tnў1[f],ј,
{tnў1[f],ј,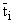 [tnўi-1[f]],ј,tnўs[f]}
є
[tnўi-1[f]],ј,tnўs[f]}
є
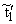 {tnў1[f],ј,tnўi-1[f],ј,tnўi-1[f],ј,tnўs[f]} ®® (по предположению индукции) ®® t0.
{tnў1[f],ј,tnўi-1[f],ј,tnўi-1[f],ј,tnўs[f]} ®® (по предположению индукции) ®® t0.
Утверждение 1
доказано.
Доказательство теоремы 1. (Ь) Пусть tn[f]n1n2јnk ®® t0 для некоторого n
> 0. Тогда, как легко видеть, tn[t]n1n2јnk ®® t0. Так как t - решение уравнения (1), то t =
tn[t], tn1n2јnk = tn[t]n1n2јnk, и по следствию
CR-теоремы имеем: tn1n2јnk ®® t0.
(Ю) Пусть tn1n2јnk ®® t0. Возможны два
случая:
a) $tў О
V0, t[f] ®® tў,
b)
Ш$tў
О V0, t[f] ®® tў.
Рассмотрим случай (a). Так как
t[f] ®® tў и tў О
V0, то t[t] ®® tў. Так как t - решение уравнения (1), то t =
t[t] и tn1n2јnk = t[t]n1n2јnk = tўn1n2јnk. Следовательно,
согласно следствию CR-теоремы, tўn1n2јnk ®® t0. Таким образом,
t[f]n1n2јnk ®® tўn1n2јnk ®® t0, и
n = 1.
Рассмотрим случай (b). Легко видеть, что t є Y(lf.t[f]) є (lh.(lx.h(xx))(lx.h(xx))) (lf.t[f]) ® (lx.(lf.t[f])(xx))(lx.(lf.t[f])(xx)) ®® (lx.t[xx])(lx.t[xx]) ® t[(lx.t[xx])(lx.t[xx])].
Следовательно, tn1n2јnk = t[(lx.t[xx])(lx.t[xx])]n1n2јnk є
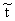 [(lx.t[xx]) (lx.t[xx])]. По следствию
CR-теоремы имеем:
[(lx.t[xx]) (lx.t[xx])]. По следствию
CR-теоремы имеем:
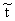 [(lx.t[xx])(lx.t[xx])] ®® t0, где число ядерных редукций равно некоторому
r, r і 0. Пусть n = r + 1. Тогда, согласно лемме 1, имеем:
[(lx.t[xx])(lx.t[xx])] ®® t0, где число ядерных редукций равно некоторому
r, r і 0. Пусть n = r + 1. Тогда, согласно лемме 1, имеем:
tn[f]n1n2јnk є
t[tn-1[f]]n1n2јnk є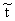 [tn-1[f]] ®® t0. [tn-1[f]] ®® t0. |
|
Теорема
1 доказана.
Теорема 2. Не
существует такого алгоритма, который по каждому уравнению (1) и термам n1,n2,ј,nk О NF0, где k і 0,
отвечает на вопрос о существовании такого n і 1,
при
котором терм tn[f]n1n2јnk имеет замкнутую нормальную
форму.
Доказательство. Проблема
существования нормальной формы для замкнутого терма, которая является
неразрешимой (см. [1]), сводится к рассматриваемой проблеме. Пусть терм t О L0. Рассмотрим
уравнение f = t[f], f О V, и
возьмем k = 0. Очевидно, что для любого n і
1 tn[f] є t[f], так как
терм t замкнут. Следовательно, вопрос о существовании требуемого n эквивалентен
вопросу о существовании нормальной формы для терма t. Теорема 2
доказана.
Теорема 3. Существует
алгоритм, который по каждому уравнению (1) и термам n1,n2,ј,nk О NF0, k і 0, таким, что
терм tn[f]n1n2јnk имеет замкнутую нормальную форму для некоторого
n і 1, строит такое n.
Доказательство следует из теоремы 1 и леммы
1.
Рассмотрим уравнение (1) и последовательность
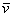 замкнутых нормальных форм
n1,n2,ј,nk, k і
0. Определим вычислительную последовательность
t1[f],ј,tn[f],ј, состоящую из нормальных форм, которую обозначим
Seq(t[f],
замкнутых нормальных форм
n1,n2,ј,nk, k і
0. Определим вычислительную последовательность
t1[f],ј,tn[f],ј, состоящую из нормальных форм, которую обозначим
Seq(t[f],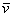 ) (если k = 0, то
Seq(t[f]) обозначает ту же последовательность, что и Seq(t[f],
) (если k = 0, то
Seq(t[f]) обозначает ту же последовательность, что и Seq(t[f],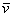 )). Последовательность
Seq(t[f],
)). Последовательность
Seq(t[f],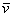 ) может быть
либо пустой, либо конечной, либо бесконечной. В бесконечной последовательности
все её члены - незамкнутые нормальные формы. Члены конечной последовательности
либо все незамкнуты, либо замкнут только последний её член. Вычислительная
последовательность Seq(t[f],
) может быть
либо пустой, либо конечной, либо бесконечной. В бесконечной последовательности
все её члены - незамкнутые нормальные формы. Члены конечной последовательности
либо все незамкнуты, либо замкнут только последний её член. Вычислительная
последовательность Seq(t[f],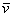 ) пуста, если терм t[f]n1n2јnk не имеет нормальной
формы. Если терм t[f]n1n2јnk имеет нормальную форму, то вычислительная
последовательность не пуста и определяется следующим
образом:
) пуста, если терм t[f]n1n2јnk не имеет нормальной
формы. Если терм t[f]n1n2јnk имеет нормальную форму, то вычислительная
последовательность не пуста и определяется следующим
образом:
t1[f] есть нормальная форма терма
t[f]n1n2јnk. Пусть уже построена подпоследовательность
t1[f],ј,ti[f], i і 1, определим, как строится еe
продолжение.
Если ti[f] О NF0 или терм ti[t[f]] не имеет
нормальной формы, то ti[f] есть последний член вычислительной
последовательности.
Если ti[f] О NF\NF0 и терм ti[t[f]] имеет
нормальную форму, то ti+1[f] есть нормальная форма терма
ti[t[f]].
Теорема 4. Пусть дано уравнение (1), его решение (2) и последовательность
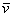 замкнутых нормальных форм
n1,n2,ј,nk, k і 0,
тогда:
замкнутых нормальных форм
n1,n2,ј,nk, k і 0,
тогда:
a) eсли вычислительная последовательность
Seq(t[f],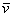 ) конечна и
имеет вид t1[f],ј,tn[f], где
tn[f] О NF0, n і 1, то tn1n2јnk ®® tn[f];
) конечна и
имеет вид t1[f],ј,tn[f], где
tn[f] О NF0, n і 1, то tn1n2јnk ®® tn[f];
b) eсли
вычислительная последовательность Seq(t[f],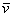 )
бесконечна, то терм tn1n2јnk не имеет нормальной
формы;
)
бесконечна, то терм tn1n2јnk не имеет нормальной
формы;
c) eсли вычислительная последовательность
Seq(t[f],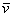 )
пуста, или
конечна и при этом имеет вид t1[f],ј,tn[f], где n і
1, tn[f] О NF\NF0 и
терм tn[t[f]] не имеет нормальной формы, то терм tn1n2јnk может как иметь, так и не иметь нормальную
форму.
)
пуста, или
конечна и при этом имеет вид t1[f],ј,tn[f], где n і
1, tn[f] О NF\NF0 и
терм tn[t[f]] не имеет нормальной формы, то терм tn1n2јnk может как иметь, так и не иметь нормальную
форму.
Доказательство. (a) Seq(t[f],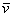 ) есть
вычислительная последовательность t1[f],ј,tn[f], где:
) есть
вычислительная последовательность t1[f],ј,tn[f], где:
|
| t[f]n1n2јnk ®® t1[f],
t1[f] О
NF\NF0, | |
| t1[t[f]] ®® t2 [f],
t2 [f]
О
NF\NF0, | |
|
| |
| |
|
| tn-2[t[f]] ®® tn-1[f],
tn-1[f] О
NF\NF0, | |
| tn-1[t[f]] ®® tn[f],
tn[f] О
NF0. | | |
| |
Легко видеть, что имеет место следующее:
|
| tn[f]n1n2јnk є t[tn-1[f]]n1n2јnk ®® t1[tn-1[f]] ®® t2 [tn-2[f]] ®® ј | |
| ј ®® tn-1[t[f]] ®® tn[f]. | | |
| |
Следовательно,
согласно теореме 1, tn1n2јnk ®® tn[f].
(b) В этом случае
вычислительная последовательность t1[f],ј,tn[f],ј бесконечна.
Покажем, что для любого n і 1 терм
tn[f]n1n2јnk имеет незамкнутую нормальную форму. Аналогично
пункту (a) имеем: tn[f]n1n2јnk ®® tn[f], где tn[f] О NF\NF0, n і 1. Таким
образом, не существует такого n і 1, что
tn[f]n1n2јnk ®® t0 и t0 О
NF0. Следовательно, согласно теореме 1, терм tn1n2јnk не имеет нормальной формы, так как он
замкнут.
(c) Перед доказательством данного пункта введем
обозначения для некоторых термов. Пусть x,y О V,
тогда:
I є lx.x, T є lxy.x, F є lxy.y, W є (lx.xx)(lx.xx),
if t1 then
t2 else t3 є
t1t2 t3, где t1,t2
,t3 О L,
й0щ є I, йn + 1щ є
lx.xFйnщ, где n = 0,1,2,ј,
Zero є lx.xT, S+ є lyx.xFy,
P- є lx.xF.
Для каждого t О L терм S+t условимся обозначать t+, а
терм P-t -
t-.
Рассмотрим
уравнение
где f
О V. Легко видеть, что последовательность Seq(W) пуста, так как терм W не имеет
нормальной формы. Не имеет нормальной формы и терм t
є Y(lf.W) є (lh.(lx.h(xx))(lx.h(xx)))(lf.W) ® (lx.(lf.W)(xx))(lx.(lf.W)(xx)) ®® (lx.W)(lx.W) ® W.
Рассмотрим
уравнение
f
= lx. if Zero x then lx.I
else (fx-)W є t[f],
где x,f О V. Покажем, что
последовательность Seq(t[f], й1щ) пуста.
t[f]й1щ є (lx. if
Zero x then lx.I else (fx-)W)й1щ ®® f й0щW, следовательно, терм t[f]й1щ не имеет нормальной формы. Однако, согласно теореме 1,
tй1щ ®® I, так
как t2[f]й1щ ®® I. Покажем это: t2
[f]й1щ є (lx. if Zero x then lx.I else ((lx. if Zero x then
lx.I else (fx-)W)x-)W)й1щ ®® ((lx. if Zero x then lx.I else (fx-)W)й0щ)W ®® (lx.I)W ® I.
Рассмотрим
уравнение
f
= lx. if Zero x then fx+ else W є t[f],
где x,f О V. Покажем, что последовательность Seq(t[f], й0щ) состоит из одного элемента
t1[f], представляющего собой незамкнутую нормальную
форму.
t[f]й0щ є (lx. if Zero x then
fx+ else W)й0щ ®® f й1щ є
t1[f] О
NF\NF0.
t1[t[f]] є (lx. if Zero x then fx+ else W)й1щ ®® W,
следовательно, терм t1[t[f]] не имеет нормальной формы. Согласно
теореме 1, не имеет нормальной формы и терм tй0щ, так как для любого n >
1 tn[f]й0щ = W.
Рассмотрим
уравнение
f = lx. if Zero x
then fx+ else (if Zero x- then (fx+)W else
lx.I) є t[f],
где x,f О V.
Покажем, что последовательность Seq(t[f], й0щ) состоит из одного элемента
t1[f], представляющего собой незамкнутую нормальную
форму.
t[f]й0щ є (lx. if Zero x then
fx+ else (if Zero x- then
(fx+)W else lx.I))й0щ ®® f й1щW є t1[f] О
NF\NF0.
t1[t[f]] є (lx. if Zero x then fx+ else (if Zero x- then (fx+)W else
lx.I))й1щ ®® fй2щW,
следовательно, терм t1[t[f]] не имеет нормальной формы. Однако,
согласно теореме 1, tй0щ ®® I, так
как t3[f]й0щ ®® I.
Теорема 4
доказана.
Теорема 5. Пусть дано
уравнение (1), его решение (2) и термы t0,n1,n2,ј,nk О NF0, где k і 0.
Пусть
tў - некоторое решение
уравнения (1). Тогда: tn1n2јnk ®® t0 Ю tўn1n2јnk ®® t0.
Доказательство. Пусть tn1n2јnk ®® t0, тогда, согласно
теореме 1, существует такое n і 1, что
tn[f]n1n2јnk ®® t0. Следовательно, и tn[tў]n1n2јnk ®® t0. Так как tў - решение уравнения (1), то tў = tn[tў], tўn1n2јnk = tn[tў]n1n2јnk и, согласно следствию CR-теоремы, tўn1n2јnk ®® t0. Теорема 5
доказана.
Теорема 6. Существует
такое уравнение (1), такое его решение tў, и такие термы t0,n1,n2,ј,nk О NF0, где k і 0,
что:
tўn1n2јnk ®® t0,
однако tn1n2јnk
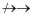 t0.
t0. | |
Доказательство. Рассмотрим уравнение f = f, где f О V, и его решение tў є lx.x.
Терм t0 є lx.x и
k = 0. Очевидно, что tў®® t0. Покажем, что терм
t не имеет нормальной формы: t
є Y(lf.f) є (lh.(lx.h(xx))(lx.h(xx)))(lf.f) ® (lx.(lf.f)(xx))(lx.(lf.f)(xx)) ®® (lx.xx)(lx.xx) є W. Теорема 6
доказана.
Ереванский государственный
университет
ЕрНИИ АСУ
Литература
1. Barendregt H.P. The Lambda
Calculus, Its Syntax and Semantics. North-Holland Pub. Comp., 1981 (рус. пер. Барендрегт Х.
Ламбда-исчисление, его синтаксис и семантика. М.: Мир, 1985).
![]() О L, y О V,
О L, y О V, ![]() [(lx.t[xx])(lx.t[xx])] ®® t0, где t0
О NF0 и число ядерных редукций равно r і 0. Тогда
[(lx.t[xx])(lx.t[xx])] ®® t0, где t0
О NF0 и число ядерных редукций равно r і 0. Тогда
![]() [tn[f]] ®® t0, если n і r.
[tn[f]] ®® t0, если n і r.![]() О L, y О V и
О L, y О V и
![]() є
є
![]() {y, ј , y},
где число свободных вхождений
переменной y в терм
{y, ј , y},
где число свободных вхождений
переменной y в терм
![]() равно k і
0.
равно k і
0.![]() {(lx.t1[xx])(lx.t1ў[xx]), ј , (lx.tk[xx])(lx.tkў[xx])} ®® t0, где t0
О NF0 и число ядерных редукций, редексы
которых получены в процессе редукции из подставленных в терм
{(lx.t1[xx])(lx.t1ў[xx]), ј , (lx.tk[xx])(lx.tkў[xx])} ®® t0, где t0
О NF0 и число ядерных редукций, редексы
которых получены в процессе редукции из подставленных в терм
![]() {y, ј , y} ядер, равно r і
0.
{y, ј , y} ядер, равно r і
0.![]() {tn1[f], ј , tnk[f]} ®® t0, если ni
і r, i = 1, ј , k.
{tn1[f], ј , tnk[f]} ®® t0, если ni
і r, i = 1, ј , k.![]() {tn1
[f], ј , tnk[f]} ®® t0. Пусть r > 0 и
утверждение 1 верно для r - 1. Докажем для r. Легко
видеть, что имеет место следующее:
{tn1
[f], ј , tnk[f]} ®® t0. Пусть r > 0 и
утверждение 1 верно для r - 1. Докажем для r. Легко
видеть, что имеет место следующее: ![]() [xx])(lx .
[xx])(lx .![]() [xx]), i = 1, ј , s, s і 1, есть все ядра,
полученные в процессе редукции из ядер, подставленных в терм
[xx]), i = 1, ј , s, s і 1, есть все ядра,
полученные в процессе редукции из ядер, подставленных в терм
![]() {y,ј,y}, и число ядерных редукций, редексами которых являются
такие ядра, равно 0. Далее мы фиксируем момент первой интересующей нас ядерной
редукции:
{y,ј,y}, и число ядерных редукций, редексами которых являются
такие ядра, равно 0. Далее мы фиксируем момент первой интересующей нас ядерной
редукции: ![]() { tnў1[f],ј,tnўi[f],ј,tnўs[f]} ®®
{ tnў1[f],ј,tnўi[f],ј,tnўs[f]} ®®
![]() {tnў1[f],ј,
{tnў1[f],ј,![]() [tnўi-1[f]],ј,tnўs[f]}
є
[tnўi-1[f]],ј,tnўs[f]}
є
![]() {tnў1[f],ј,tnўi-1[f],ј,tnўi-1[f],ј,tnўs[f]} ®® (по предположению индукции) ®® t0.
{tnў1[f],ј,tnўi-1[f],ј,tnўi-1[f],ј,tnўs[f]} ®® (по предположению индукции) ®® t0.![]() [(lx.t[xx]) (lx.t[xx])]. По следствию
CR-теоремы имеем:
[(lx.t[xx]) (lx.t[xx])]. По следствию
CR-теоремы имеем:
![]() [(lx.t[xx])(lx.t[xx])] ®® t0, где число ядерных редукций равно некоторому
r, r і 0. Пусть n = r + 1. Тогда, согласно лемме 1, имеем:
[(lx.t[xx])(lx.t[xx])] ®® t0, где число ядерных редукций равно некоторому
r, r і 0. Пусть n = r + 1. Тогда, согласно лемме 1, имеем:
![]() замкнутых нормальных форм
n1,n2,ј,nk, k і
0. Определим вычислительную последовательность
t1[f],ј,tn[f],ј, состоящую из нормальных форм, которую обозначим
Seq(t[f],
замкнутых нормальных форм
n1,n2,ј,nk, k і
0. Определим вычислительную последовательность
t1[f],ј,tn[f],ј, состоящую из нормальных форм, которую обозначим
Seq(t[f],![]() ) (если k = 0, то
Seq(t[f]) обозначает ту же последовательность, что и Seq(t[f],
) (если k = 0, то
Seq(t[f]) обозначает ту же последовательность, что и Seq(t[f],![]() )). Последовательность
Seq(t[f],
)). Последовательность
Seq(t[f],![]() ) может быть
либо пустой, либо конечной, либо бесконечной. В бесконечной последовательности
все её члены - незамкнутые нормальные формы. Члены конечной последовательности
либо все незамкнуты, либо замкнут только последний её член. Вычислительная
последовательность Seq(t[f],
) может быть
либо пустой, либо конечной, либо бесконечной. В бесконечной последовательности
все её члены - незамкнутые нормальные формы. Члены конечной последовательности
либо все незамкнуты, либо замкнут только последний её член. Вычислительная
последовательность Seq(t[f],![]() ) пуста, если терм t[f]n1n2јnk не имеет нормальной
формы. Если терм t[f]n1n2јnk имеет нормальную форму, то вычислительная
последовательность не пуста и определяется следующим
образом:
) пуста, если терм t[f]n1n2јnk не имеет нормальной
формы. Если терм t[f]n1n2јnk имеет нормальную форму, то вычислительная
последовательность не пуста и определяется следующим
образом:![]() замкнутых нормальных форм
n1,n2,ј,nk, k і 0,
тогда:
замкнутых нормальных форм
n1,n2,ј,nk, k і 0,
тогда:![]() ) конечна и
имеет вид t1[f],ј,tn[f], где
tn[f] О NF0, n і 1, то tn1n2јnk ®® tn[f];
) конечна и
имеет вид t1[f],ј,tn[f], где
tn[f] О NF0, n і 1, то tn1n2јnk ®® tn[f];![]() )
бесконечна, то терм tn1n2јnk не имеет нормальной
формы;
)
бесконечна, то терм tn1n2јnk не имеет нормальной
формы;![]() )
пуста, или
конечна и при этом имеет вид t1[f],ј,tn[f], где n і
1, tn[f] О NF\NF0 и
терм tn[t[f]] не имеет нормальной формы, то терм tn1n2јnk может как иметь, так и не иметь нормальную
форму.
)
пуста, или
конечна и при этом имеет вид t1[f],ј,tn[f], где n і
1, tn[f] О NF\NF0 и
терм tn[t[f]] не имеет нормальной формы, то терм tn1n2јnk может как иметь, так и не иметь нормальную
форму.![]() ) есть
вычислительная последовательность t1[f],ј,tn[f], где:
) есть
вычислительная последовательность t1[f],ј,tn[f], где: