МАТЕМАТИКА
УДК 519.65, 517.57
Академик А. Б. Нерсесян
Квазиэкспонента и квазипреобразования Фурье
(Представлено 30/XI 2000)
1.Пусть z О
Cm, m і 1. Через
{zk}(k = 1,2,ј, m) обозначим компоненты z,
через zw(z/w) обозначим вектор с компонентами
{zkwk}({zk/wk}), а через < z,w
> - скалярное произведение еzk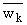 (|z|2 = < z,z >). Будем также считать, что z
№ 0, z > 0, z О
Rm, z = Ґ, z - целое, четное и т. п.,
если таковы все компоненты z. Если в сумме
(|z|2 = < z,z >). Будем также считать, что z
№ 0, z > 0, z О
Rm, z = Ґ, z - целое, четное и т. п.,
если таковы все компоненты z. Если в сумме
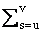 u и v целые и u Ј v, то предполагается суммирование по всем целым компонентам
s, таким, что u Ј s Ј
v.
u и v целые и u Ј v, то предполагается суммирование по всем целым компонентам
s, таким, что u Ј s Ј
v.
Зафиксировав теперь неотрицательное A и положительное N,
рассмотрим функцию q, именуемую в дальнейшем базовой (s - целое) 1
| q = q(l,s) = q(l, s,
N), l О Cm, s О Rm, q
О C | |
(1) |
Будем
предполагать, что q удовлетворяет одному из следующих
условий:
| d1(l) = |
Ґ
е
s=-Ґ
|
|q(l,s)| ep <
Ns,A > < Ґ, | |
(2) |
| d2(l) =
|
Ґ
е
s=-Ґ
|
|q(l,s)|2 e2p < Ns,A > < Ґ. | |
(3) |
Основным объектом
дальнейшего изучения является функция e(l, x), -
назовем ее квазиэкспонентой, - формально определяемая
рядом
| e(l,x) = e(l,x,N,q) = |
Ґ
е
s=-Ґ
|
q(l, s) eip
< l+Ns,x >
| |
(4) |
Очевидно, что при
выполнении условия (2) e(l, x) локально непрерывна по x
О
Cm, |Im x|
Ј A.
Лемма 1. Если k О Rm -
целое и выполнено
условие (2), то
| e(l,x + 2k/N) =
e2ip < l,k/N > e(l,x). | |
(5) |
Для данного T О Rm, T > 0, обозначим
| DT = {x О
Rm,|xk| Ј
Tk, k = 1,2,јm}. | |
(6) |
Лемма 2.
Если функции q1 = q1(l, s), q2 = q2(l, s) удовлетворяют
условиям (3) и параметры T,p,q О Rm - целые,
то
|
у
х |
DT
|
e(p,x,q1) |
e(q,x,q2)
|
dx = 2m |
ж
и |
m
Х
k=1
|
Tk |
ц
ш |
|
ж
и |
Ґ
е
s=-Ґ
|
q1(p,s) |
q2(q,s)
|
ц
ш |
dp,q, | |
(7) |
где dp,q - символ
Кронекера.
2. Обозначим
теперь
| r(x) = r(x,N) = |
у
х |
DN/2
|
e(l,x)dl, x О
Cm, |Imx| Ј
A | |
(8) |
и назовем эту функцию опорной. Функция r(x) существует, - и
даже непрерывна, - если выполнено условие (2).
Введем в
рассмотрение также функцию m, фактически отличающуюся
от функции q только другой формой записи
|
| m(l) = m(l,N) = q(u,n,N), | |
| Reu = Rel(Mod N), u О DN, n = (l - u)/N,l
О
Cm. | | |
| |
(9) |
Нетрудно видеть, что, при -N/2 Ј Rel
Ј N/2, q(l,s) = m(l + Ns).
Лемма 3. Если m = m(l) = m(l, N)
О L2(Rm) и выполнено условие (2),
то
r(x) = r(x,N) = 2m/2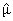 |
= |
у
х |
DRm
|
eip
< l,x > m(l,N)dl, l О Rm, | |
(10) |
где использован символ
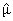 преобразования Фурье от m
2.
преобразования Фурье от m
2.
Наряду с
леммами 1 и 2 отметим также следующий аналог известного свойства
экспоненты.
Лемма 4. Если q определяется формулой (11), где m
не зависит от N, то для 0 < k О Rm
Переобозначим базовую функцию q как зависящую
от двух дополнительных параметров a и b следующим образом:
| q(l,s) = q(l,s,N,a,b) = m(a(l/N + s),N)eip
< b,s >
, | |
(12) |
где N,a,b О
Rm, a > 0, bk О [0,2p), (k = 1,2, .ј, m).
Предположим теперь, что 0 Ј L О R, r(x) кусочно-непрерывна и ряд
|
Ґ
е
s=-Ґ
|
epLsr(x - 2s - b,N), |Im x| Ј
A | |
абсолютно и равномерно
сходится по x на каждом компакте в Rm. Отметим, что в одномерном
случае (m = 1) и при A = 0, согласно известной лемме Харди (см.[1]), достаточно
потребовать, чтобы r(x) О
L1(R) имела ограниченную вариацию и была нормирована как r(x) = (r(x + 0) + r(x - 0)) / 2.
Центральным результатом данной работы
является
Теорема 1. При |Im x| Ј A и |Im l| Ј L
квазиэкспонента представима в виде
| e(l,x) = a-1e-ip < l/N,b > |
Ґ
е
s=-Ґ
|
r(a-1(Nx - 2s - b))e2ip <
l,s/N > . | |
(13) |
3. Если выполнено условие (2), обозначим
| ag(l)= |
Ґ
е
s=-Ґ
|
eip
< s,g > q(l,s), -1 Ј g Ј
1. | |
(14) |
Нетрудно видеть, что
при ag(l) № 0 функция ag(l)-1e(l,x) является интерполяцией экспоненты eip < l,x > на сетке
{(2k + g) / N}, где k - произвольное целое. Пусть теперь
задана некоторая ограниченная комплекснозначная функция w = w(l) = w(l,
N), l О Cm, w О C.
Теорема 2.
Пусть выполнено условие (2). Тогда при любом x
О
Cm
|
| |eip < l,x
> - w(l)e(l,x)| Ј exp(p(Re(l)Im(x) - Re(x)Im(l))) | |
|
ж
и
|
|1 - w(l)q(l,0)| + |w(l)| |
Ґ ~
е
s=-Ґ
|
|q(l,s)|ep < Ns,Imx > |
ц
ш
|
, |Im x|
Ј
A, | | |
| |
(15) |
где символ
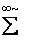 означает, что s №
0.
означает, что s №
0.
Теорема 3. Пусть выполнено
условие (3) и 0 < T О Rm. Тогда
|
|
у
х
|
DT
|
|eip < l,x
> - w(l)e(l,x)|2dx Ј 2m |
ж
и
|
m
Х
k=1
|
([Tk] + 1)e2pTk|Im lk| |
ц
ш
|
, | |
|
ж
и
|
|1 - w(l)q(l,0)|2 + |w(l)|2 |
Ґ ~
е
s=-Ґ
|
|q(l,s)|2 |
ц
ш
|
, | | |
| |
(16) |
где [Tk] - целая часть
Tk и символ
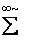 означает, что s
№ 0.
означает, что s
№ 0.
В частности,
при w = (ag)-1 теоремы 1 и 2
характеризуют близость интерполирующей функции w(l)e(l,x) к
экспоненте.
4. В дальнейшем, - ради
простоты формул, - будем считать, что l, x О Rm, d2(l) № 0 и выполнены условие (3) и
представления (12), (13) при A = 0,a = 1,b = 0.
Теорема 4. Правая часть оценки (16) принимает минимальное значение при
Введем в рассмотрение функцию
| e0(l,x) = 2-m/2d2(l)-1/2e(l,x). | |
(18) |
Квазипреобразованиями
Фурье (соответственно прямым и обратным) назовем операторы
| (Ff)(x) = |
у
х |
DN/2
|
e0(l,x)f(l)dl, f О
L2(DN/2), | |
(19) |
| (Yg)(l) = |
у
х |
Rm
|
|
e0(l,x)
|
g(x)dx, g О
L2(Rm). | |
(20) |
Для функции f(l) О L2(DN/2)
через fN(l) О
L2 loc обозначим ее N-периодическое продолжение на
Rm (т. е. Nk - периодическое продолжение по каждой
компоненте lk).
Лемма 5.
При q(l) О Cloc
| Ff = (d2(l)-1/2m(l/N)fN(l))Щ О L2(Rm), f(l) О
L2(DN/2). | |
(21) |
Лемма 6.
При m(l) О Cloc для любых f
О L2(DN/2) и g О L2(Rm) справедливы соотношения
| ||Ff||1 = ||f||2, ||Yg||2 Ј ||g||1, | |
(22) |
где ||.||1 и ||.||2 -
нормы в L2(Rm) и
L2(DN/2) соответственно.
Таким образом, F :
L2(Rm) ®
L2(DN/2) и Y :
L2(DN/2) ®
L2(Rm), причем отображение F
изометрично, а Y не увеличивает норму. На самом деле
отображение Y есть обратное к F, что является следствием следующего, более общего,
результата.
Теорема 5. Пусть
отображение F1 соответствует базовой функции
q1, определяемой m1 согласно (9), а отображение Y2 - базовой функции q2, определяемой m2. Предположим, что q1 удовлетворяет условиям леммы 4, q2 - условию (3). Тогда
где
| s12(l) = (d2(l,m1)d2(l,m2))-1/2 |
Ґ
е
s=-Ґ
|
m1(s + l/N)m2(s + l/N), | |
причем
|s12(l)| Ј 1 и только при m1 є
m2 имеем s12(l) є 1.
Оказывается, что
отображения F и Y являются
аппроксимациями классического преобразования Фурье (соответственно прямого и
обратного).
Теорема 6. Пусть
m(l) О L2(Rm) и выполнено условие (3). Тогда
для любого f О L2(Rm)
где в Ff
использовано сужение f(l) на DN/2,
а ||.||1 и fN(l)
определены, как в леммах 4 и 5.
Теорема 7. Пусть g О L2(Rm)
и выполнено условие (3). Тогда
|
| ||ğ - Yg||2 Ј ||ğ(l)(1 - |
d2(l)-1/2
|
|
m(l/N)
|
)||2 + | |
|
|
| ||d2(l)-1/2 |
Ґ ~
е
s=-Ґ
|
ğ(l + Ns) |
m(l/N + s)
|
||2 Ј | |
|
|
|
ж
и
|
у
х
|
DN/2
|
|1 - d2(l)-1/2m(l/N)|2dl |
ц
ш
|
||g||1 + |
у
х
|
Rm\DN/2
|
|g(x)|2dx, | | |
| |
(25) |
где
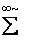 , ||.||1 и ||.||2 определены, как в теореме 1 и лемме 4
соответственно.
, ||.||1 и ||.||2 определены, как в теореме 1 и лемме 4
соответственно.
Следующие двойственные
представления операторов F и Y
вытекают из формулы (13).
Теорема 8. В условиях леммы 3 для любых f О
L2(DN/2) и g О
L2(Rm)
| (Ff)x = |
Ґ
е
s=-Ґ
|
r(Nx - 2s) |
у
х |
DN/2
|
eip
< l,2s/N > d2(l)-1/2f(l)dl, | |
(26) |
| (Yg)(l) = d2(l)-1/2 |
Ґ
е
s=-Ґ
|
eip
< l,2s/N > |
у
х |
Rm
|
r(Nx - 2s)g(x)dx. | |
(27) |
5. Общеизвестна фундаментальная роль экспоненты Фурье
eixl как в теоретических, так и
прикладных дисциплинах. Достаточно упомянуть аппарат рядов и преобразований
Фурье, чтобы подчеркнуть важность оптимизации вычислительных процессов,
связанных с экспонентой. Такой современный метод разработки быстрых алгоритмов,
как теория вейвлетов, по сути, связан с анализом Фурье, т. е., в конечном
счете, с той же экспонентой (см., например,
[4-6]).
Приведенный подход основан на общем методе работы
[6]. Исходное представление квазиэкспоненты (4) удобно для оценки ошибки от
замены экспоненты квазиэкспонентой, в то время как формула (13) гораздо
эффективнее для вычисления значений квазиэкспоненты и может служить основой
быстрых алгоритмов, поскольку, с одной стороны, она содержит оператор
дискретного преобразования Фурье, а с другой - сжатия и сдвиги определенной
функции r. Понятно, что случай, когда r(x) имеет финитный ("почти финитный" - относительно заданной
точности) носитель, наиболее интересен. Отметим, что при целом l приведенные результаты содержат схему построения
периодических вейвлетов на отрезке [-1,1] (см. [2], a также
[3-5]).
Возможности приложения свойств квазиэкспоненты
довольно многообразны. Здесь мы не будем их перечислять, а укажем только
алгоритмы быстрого вычисления рядов и классических преобразований Фурье (см.
теоремы 5-8), а также дискретных преобразований Фурье на неравномерных сетках
(НДПФ)(см. теорему 1).
В последнем случае предлагаемая
схема, в отличие от известных (см. [7,8]), позволяет практически точно оценить
ошибку от замены экспоненты квазиэкспонентой. Реализованы соответствующие
быстрые НДПФ-алгоритмы, ориентированные на заданную
точность.
Численные эксперименты подтверждают
перспективность эффективного применения квазиэкспоненты в ряде других задач.
Институт математики НАН РА
Литература
1. Тиман А.Ф. Теория
приближения функций действительного переменного. М.: Физматгиз, 1960. 624
с.
2. Daubechies I. Ten
lectures of wavelets. CBMS-NSF Series of Appl. Math., SIAM Publications,
Philadelfia. 1992.
3. Edelman A.,
McCourcodale P., Toledo S. - SIAM J. Sci. Comput. 1999.
V. 20. № 3. P. 1094-1114.
4. Locher F. -
Math. Comput., 1995. V. 64. № 210. P.
671-690.
5. Нерсесян А.Б. - ДНАН Армении. 1998. Т. 98. № 1. С. 23-30.
6. Nersessian A. - Numer. Funct.Anal. and Optimization. 2000.
V. 21(1&2). P. 227-240.
7. Dutt A.,
Rokhlin V. - SIAM J. Sci. Statist. Comput. 1993. V. 14. № 6.
P. 1368-1393.
8. Ware A.F. - SIAM Review. 1998. V. 40. № 4. P. 838-856.
Footnotes:
1Здесь и далее в определениях функций будем указывать все ее аргументы,
опуская некоторые из них впоследствии.
2Будем пользоваться также общеизвестным символом обратного преобразования
Фурье (m = 2-m/2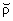 ).
).
![]() преобразования Фурье от m
2.
преобразования Фурье от m
2.![]() означает, что s
№ 0.
означает, что s
№ 0.