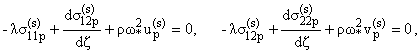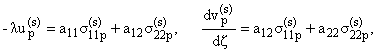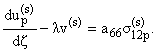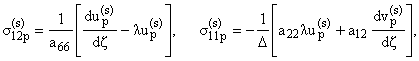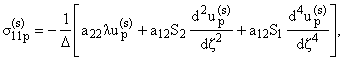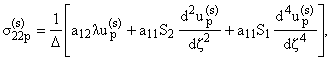ТЕОРИЯ УПРУГОСТИ
УДК 539.3
Академик Л. А. Агаловян, Л. Г. Гулгазарян
О характере пограничного слоя
при собственных
колебаниях ортотропной полосы
(Представлено 11/V 2000)
Собственным колебаниям ортотропной полосы
посвящены работы [1, 2], в которых найдены частоты собственных колебаний и
установлены связи между ними и скоростями распространения сейсмических сдвиговых
и продольных волн. Случай общей анизотропии рассмотрен в
[3]. Собственные колебания ортотропной полосы при смешанных граничных
условиях рассмотрены в [4], а двухслойной ортотропной полосы в [5-7].
Пограничный слой в задаче о собственных колебаниях полосы, когда одна из
продольных кромок жестко закреплена, а другая свободна, рассмотрен в [8]. В
[9] изучен пограничный слой в задаче о собственных колебаниях двухслойной
изотропной полосы при неполном контакте между слоями.
В работе рассматриваются собственные
колебания ортотропной полосы в зоне пограничного слоя, выведено уравнение для
определения показателей, характеризующих скорость затухания величин
погранслоя. Показано, что каждой частоте собственных колебаний
соответствует отдельный класс пограничных функций.
При исследовании собственных колебаний
ортотропной полосы W = { (x, y) : x
О [0, l], |y| Ј h, h << l}
однородные динамические уравнения плоской задачи [10, 11] приводятся к
сингулярно возмущенной малым параметром e = h / l системе
уравнений. Решение этой системы складывается из решений внутренней задачи и
пограничного слоя. Количество произвольных констант в решении внутренней
задачи недостаточно для удовлетворения краевым условиям на боковой поверхности
полосы. Возникающая неувязка устраняется с помощью качественно нового
решения - пограничного слоя.
Частоты w собственных колебаний ортотропной полосы определяются из
решения внутренней задачи [1], в частности, когда на лицевых поверхностях заданы
условия
они определены в [4]
и связаны со скоростями распространения сейсмических сдвиговых и продольных волн
Vs и Vp следующим образом:
|
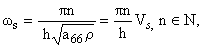 |
|
|
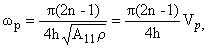 |
|
|
| A11 = (a11a22 - a122)/a11
, | | |
| |
(1.3) |
где ws частота собственных сдвиговых колебаний, а
wp - продольных колебаний.
Для построения решения пограничного слоя в
динамических уравнениях для ортотропной полосы введем новые переменные h = x / h, z = y / h, и решение будем искать в виде Qik = Qikp(h, z)eiwt, где Qikp - любая из искомых
величин. В результате получим систему уравнений
|
| e-1 |
¶s11p
¶h
|
+ e-1 |
¶s12p
¶z
|
+ e-2rw*2up = 0
, e-1 |
¶s12p
¶h
|
+ e-1 |
¶s22p
¶z
|
+ e-2rw*2vp = 0
, | |
|
|
| e-1 |
¶up
¶h
|
= a11s11p + a12s22p ,
e-1 |
¶vp
¶z
|
= a12s11p + a22s22p ,
| |
|
|
| e-1 |
¶up
¶z
|
+ e-1 |
¶vp
¶h
|
= a66s12p ,
| | |
| |
(1.4) |
где aik - коэффициенты
упругости, r - плотность слоев, up = u / l , vp = v / l - безразмерные компоненты вектора перемещения, w*2 = w2h2. Решение системы (1.4) будем
искать в виде
|
| Qikp= |
N
е
s=0
|
eqik+sQikp(s)(z)e-lh | | |
| |
(1.5) |
где qik характеризуют
асимптотические порядки искомых величин. Считается, что
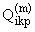 = 0, если m < 0. Подставив (1.5) в (1.4),
получим непротиворечивую систему относительно
= 0, если m < 0. Подставив (1.5) в (1.4),
получим непротиворечивую систему относительно
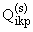 ,
если qik = -1 для напряжений, qik = 0
для перемещений. В результате имеем
,
если qik = -1 для напряжений, qik = 0
для перемещений. В результате имеем
Из
этой системы напряжения выражаются через компоненты вектора перемещения по
формулам
а для определения перемещений
up(s), vp(s) получается система
|
| l11up(s) - l12vp(s) = 0, l22vp(s) - l12up(s) = 0
, | | |
| |
(1.8) |
где операторы lik имеют
вид
|
| l12 = l(Δ -a12a66) |
d
dz
|
,
l22 = a11a66 |
d2
dz2
|
+ Δ (l2 + a66w*2r) , | |
|
|
| l11 =
Δ |
d2
dz2
|
+ (l2a22 + w*2rΔ)a66
. | | |
| |
(1.9) |
Из
системы (1.8) следует уравнение
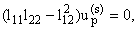 которое в развернутом виде имеет вид
которое в развернутом виде имеет вид
|
| a11 |
d4up(s)
dz4
|
+ |
й
л
|
(Δ
+ a11a66)w*2r + (a66 + 2a12)l2 |
щ
ы
|
× | |
|
|
| × |
d2up(s)
dz2
|
+ (l2a22 + w*2rΔ )(l2 + a66w*2r)up(s) = 0
, | | |
| |
(1.10) |
а для
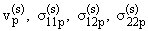 из системы (1.8) и из (1.7)
получаются
из системы (1.8) и из (1.7)
получаются
|
| vp(s) = S1 |
d3up(s)
dz3
|
+ S2 |
dup(s)
dz
|
, s12p(s) = |
1
a66
|
|
й
л
|
(1 - lS2) |
dup(s)
dz
|
- lS1 |
d3up(s)
dz3
|
|
щ
ы
|
,
| |
|
|
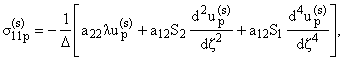 |
|
|
|
|
| S1 = - |
a11a66
l(Δ - a12a66)(l2 + a66w*2r)
|
, | |
|
|
| S2 = - |
(l2((a66 + a12)2 - a11a22) + w*2ra11a662)
l(Δ - a12a66)(l2 + a66w*2r)
|
.
| | |
| |
(1.11) |
Решением уравнения (1.10) является
|
| up(s) = C1cosz1lz + C2sinz1lz + C3cosz2lz +
C4sinz2lz ,
| |
|
|
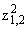 = ((Δ
+ a11a66)m2r + a66 + 2a12 ± = ((Δ
+ a11a66)m2r + a66 + 2a12 ±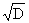 )/(2a11) ,
m = w*/l , )/(2a11) ,
m = w*/l ,
| | |
| |
(1.12) |
|
| D = (Δ - a11a66)2m4r2
+ (2(a66 + 2a12)(Δ
+ a11a66) -
| |
|
|
| - 4a11a22a66 - 4a11Δ )m2r + (a66 + 2a12)2 - 4a11a22
. | | |
| |
(1.13) |
Подставив (1.12) в (1.11) и в граничные условия (1.1), (1.2), получим
однородную систему алгебраических уравнений относительно неизвестных
C1, C2, C3, C4, для существования
нетривиальных решений которой необходимо, чтобы ее определитель равнялся нулю,
вследствие чего получается трансцендентное уравнение (1.14), откуда определяется
показатель экспоненты l
|
| (B2D1 + B1D2)sin2l(z1 - z2) + (B2D1 - B1D2)sin2l(z1 + z2) = 0
, | |
|
|
| Bi = 1/Δ
(a11aizi + a12)
,
Di = 1/a66(zi + Ai)
, | |
|
|
| Ai= |
a11a66zi3 - ((a66 + a12)2 - a12a22 + m2ra11a662)zi
(a12a66 - Δ )(1 + a66m2r)
|
, i = 1,
2 . | | |
| |
(1.14) |
В
частности, для пограничного слоя изотропной полосы имеем уравнение
|
| (1 + Q)sin2l(z1 - z2) + (1 - Q)sin2l(z1 + z2) = 0
, | |
|
|
| z12 = 1 + m2r |
1 - n2
E
|
,
z22 = 1 + 2m2r |
1 + n
E
|
, Q = |
(1 + z22)2
4z1z2
|
,
| | |
| |
(1.15) |
где n -
коэффициент Пуассона, E - модуль упругости.
В уравнение (1.14) в качестве параметра входит w, и каждому его значению из (1.3) будет соответствовать
счетное множество l. В силу свойства пограничного
слоя необходимо ограничиться теми значениями l, у
которых Re l > 0. Таким образом, каждому
собственному значению w соответствует свое семейство
пограничных функций. В табл. 1,2 приведены некоторые первые значения
l для ортотропной полосы из материала СВАМ 10:1 с
характеристиками a11 = 2.614 · 10-11Па-1, a22 = 5.669 · 10-11Па-1, a66 = 19.234 · 10-11Па-1,
a12 = -0.575 · 10-11Па-1, в табл. 3,4 - для изотропной полосы из
железобетона с характеристиками E = 206 · 108 Па, n = 0.2.
Из (1.14) или
(1.15), определив l, по формулам (1.11), (1.12)
определяются все компоненты тензора напряжений и вектора перемещения погранслоя.
Как следует из (1.5), величины погранслоя
затухают экспоненциально, а показатели экспонент определяются из (1.14) или
(1.15). Из табл. 1-4 следует, что реальные части показателей экспонент
возрастают достаточно быстро и в прикладных вычислениях можно ограничиться
первыми несколькими корнями этих уравнений.
Сопряжение решений пограничного слоя и внутренней задачи, в частности,
можно осуществить методом наименьших квадратов или методом граничной коллокации
[10, 11].
Таблица 1
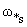 = pn / = pn /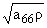 |
|
|
| n=1 |
l1=0.24019+1.0318 i
|
l3=2.211749
|
|
l2=1.404897 |
l4=2.7294+0.23825 i |
|
|
| n=2 |
l1=1.89794 |
l3=3.417765 |
|
l2=2.95038+0.1825 i |
l4=4.22615 |
|
|
| n=3 |
l1=2.308669 |
l3=4.097049 |
|
l2=3.12928+0.2095 i |
l4=4.912268 |
|
|
| n=4 |
l1=2.7104+0.19626 |
l3=4.64799 |
|
l2=3.65966 |
l4=5.51521 |
|
|
| n=5 |
l1=2.6232+0.06136 i |
l3=5.135879 |
|
l2=4.091669 |
l4=6.05979 |
|
Таблица 2
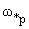 = p(2n-1) / = p(2n-1) / |
|
|
| n=1 |
l1=1.025788 |
l3=2.385279 |
|
l2=1.725649
|
l4=3.043771
|
|
|
| n=2 |
l1=0.519403 |
l3=2.53485 |
|
l2=1.72838 |
l4=3.260538 |
|
|
| n=3 |
l1=1.048913 |
l3=3.213979 |
|
l2=2.314626 |
l4=4.007347 |
|
|
| n=4 |
l1=1.530886 |
l3=3.829277 |
|
l2=2.854538 |
l4=4.682892 |
|
|
| n=5 |
l1=2.00026 |
l3=4.406754 |
|
l2=3.36996 |
l4=5.313287 |
|
Таблица 3
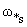 = pn / = pn /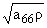
|
|
|
| n=1 |
l1=0.38976 |
l3=5.2191+0.96275 i |
|
l2=3.3477+0.86728 i |
l4=6.9429+1.02561 i |
|
|
| n=2 |
l1=4.30501+0.3295 i |
l3=7.238734+0.66865 i |
|
l2=5.72599 |
l4=9.14279+0.89291 i |
|
|
| n=3 |
l1=3.76542 |
l3=8.260449+0.81639 i |
|
l2=5.8695+0.61608 i |
l4=10.34442+0.81351 i |
|
|
| n=4 |
l1=3.208627 |
l3=9.099352+0.546398 i |
|
l2=6.4035+0.7167 i |
l4=10.784599 |
|
|
| n=5 |
l1=2.002788 |
l3=8.920408 |
|
l2=6.78042+0.43728 i |
l4=10.6919+0.54696 i |
|
Таблица 4
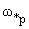 = p(2n-1) / = p(2n-1) / |
|
|
| n=1 |
l1=2.46428+0.78908 i |
l3=5.7563+0.96983 i |
|
l2=4.13907+0.8955 i |
l4=7.3539+1.02711 i |
|
|
| n=2 |
l1=2.88329+0.76794 i |
l3=6.73414+1.009398 i |
|
l2=4.93595+0.930545 i |
l4=8.44149+1.06455 i |
|
|
| n=3 |
l1=4.40205+0.18667 i |
l3=7.289697+0.707421 i |
|
l2=5.678714 |
l4=9.18057+0.909667 i |
|
|
| n=4 |
l1=3.941194+0.47119 i |
l3=8.84117+0.75743 i |
|
l2=6.65485+0.7855 i |
l4=10.8455+0.58944 i |
|
|
| n=5 |
l1=5.3607+0.50225 i |
l3=8.9335+0.50455 i |
|
l2=7.413001 |
l4=11.12814+0.81348 i |
|
Институт механики НАН РА
Литература
1. Агаловян Л. А. - В сб.: Юбил. научн. конф. к 60-летию ГПИ. Гюмри, 1994.
2. Агаловян M. Л. - ДНАН Армении. 1996. Т. 96. № 2-4. С. 23-28.
3. Агаловян M. Л. - Уч. зап. ЕГУ. 1997. N 2. (187).
4. Гулгазарян Л. Г. - Изв. НАН Армении. Механика. 1999. Т. 52. № 4.
5. Агаловян Л. А., Саркисян Л.
С. - Тр. XVIII Междунар. конф. по теории оболочек и пластин.
РФ. Саратов. Т. 1. 1997.
6. Саркисян Л. С. - ДНАН Армении. 1997. Т. 97. № 3.
С. 19-25.
7. Гулгазарян Л.
Г. - Материалы респ. конф. молодых ученых. Ереван, 1999.
8. Агаловян М. Л. - В сб.: Вопросы оптимального управления, устойчивости и прочности
механических систем. Ереван, 1997.
9. Гулгазарян Л. Г. - Изв. НАН Армении. Механика. 2000. Т.
53. № 2.
10. Агаловян Л. А. -
Асимптотическая теория анизотропных пластин и оболочек. М.: Наука,
1997.
11. Лурье А. Н. - Теория упругости. М.: Наука, 1970.
![]() = 0, если m < 0. Подставив (1.5) в (1.4),
получим непротиворечивую систему относительно
= 0, если m < 0. Подставив (1.5) в (1.4),
получим непротиворечивую систему относительно
![]() ,
если qik = -1 для напряжений, qik = 0
для перемещений. В результате имеем
,
если qik = -1 для напряжений, qik = 0
для перемещений. В результате имеем