ИНФОРМАТИКА
УДК 57.082.14
А. Э. Геворкян
Осуществление сопряженной модели трехферментной
цепи с
тремя ферментами в комплексе с помощью
пакета динамического моделирования
"Stella"
(Представлено академиком Ю. Г. Шукуряном 3/XI 2000)
Математическая теория анализа
регуляции ферментов. Хорошо известно [1, 2], что простейшая
ферментативная реакция (один фермент - один субстрат) может быть представлена
следующей двухфазной реакцией:
где S, E,
SE и P являются концентрациями соответственно субстрата, фермента,
фермент-субстратного комплекса и продукта реакции. При кинетических
исследованиях основная роль отводится определению констант скоростей процесса
(K1, K2, K3, K4). Обобщая эту
схему для цепей реакций с более чем одним ферментом, получим:
|
| S + E1 |
K21
|
E1S |
K41
|
P1 + (E1) + E2 |
K22
|
E2P1 |
K42
|
P2 + (E2) + E3 ј | |
| ј |
K4i
|
Pi + (Ei) + Ei+1 |
K2i+2
|
Ei+1Pi |
K4i+1
|
Pi+1 + Ei+1 ј | | |
| |
где
Ei - концентрации всех участвующих в реакции
ферментов, Pi - концентрации промежуточных продуктов
(i = 2јn, n - любое натуральное
число). В этом случае каждый шаг цепи характеризуется собственной четверкой
констант скоростей. Ранее обсуждалось образование фермент-субстратных
комплексов и их поведение в аналогичной цепи, состоящей из трех ферментов,
функционирующих независимо (изолированно) друг от друга [3]. Ферменты
действуют изолированно (или независимо), пока функционирование хотя бы одного
фермента в цепи не влияет на кинетические параметры образования продукта,
находящегося под подчинением другого фермента.
Теория анализа регуляции ферментов учитывает взаимодействие метаболитов,
являющихся промежуточными продуктами, с более чем одним ферментом. Ферменты
вступают во взаимодействие друг с другом благодаря этим общим метаболитам, и,
следовательно, ферментативная активность в каком-либо каталитическом центре
приводит к изменению локальных скоростей всех ферментов, взаимодействующих с
этим метаболитом. Таким образом, становится невозможным определение
воздействия одного фермента на течение данной реакции в цепи без учета
взаимодействий сопряженных с ним других ферментов. В литературе отмечаются
случаи [4], когда становится возможным нахождение констант равновесия
воздействия фермент-ферментного комплекса при дальнейшем его рассмотрении как
одного фермента с несколькими активными центрами. Теория анализа регуляции
ферментов учитывает также невозможность определения констант равновесия и
обеспечивает взаимодействие двух и более ферментов математической теорией [4], в
основе которой лежит идея параметра гибкости, с помощью которого описывается
вклад (мера участия) каждого фермента в фермент-ферментном
взаимодействии. Согласно определению [5], параметр гибкости является
частным производным скорости реакции по концентрации фермента, умноженным на
коэффициент E/v, где E - концентрация фермента, v - локальная скорость реакции.
|
| pvE = |
E
v
|
|
ж
з
и
|
|
¶v
¶E
|
|
ц
ч
ш
|
= |
¶lnv
¶lnE
|
. | | |
| |
В любой фиксированный момент времени t данное частное производное
отождествляется с обычным производным, так как остаются постоянными все другие
параметры и для определения параметра гибкости достаточно пользоваться следующим
свойством обычного производного:
|
| pvE = |
d lnv
d lnE
|
= |
d lnv
d lnt
|
/ |
d lnE
d lnt
|
(для любого
дискретного момента t).
| | |
| |
(1) |
Параметры гибкости меняют локальную скорость соответствующей реакции
цепи, прибавляясь к константе скорости K3 продукта образования этих
реакций, соответственно ускоряя (когда p > 0) или
замедляя (когда p < 0) реакцию. При
изолированном функционировании ферментов параметр гибкости всегда равен 0, в то
время как в сопряженном комплексе ферментов соответствующие параметры p приобретают разные от 0 значения.
Описание
модели. Ниже приводится описание сопряженной модели ферментов с
помощью пакета динамического моделирования "Stella" на примере трехферментной
цепи с тремя ферментами в комплексе.
Четырьмя основными предположениями функционирования сопряженной модели {E1-E2-E3} являются:
1. производное концентраций прямо
пропорционально скорости реакции;
2. концентрации ферментов имеют намного более низкий порядок, чем
концентрации субстратов;
3. общая
концентрация фермента постоянна в течениe реакции и равна сумме свободного
фермента и фермент-субстратного комплекса в любой момент времени;
4. в основе взаимодействия сопряженных
ферментов лежит воздействие всех трех возможных пар ферментов: {E1-E2}, {E2-E3} и {E1-E3}. При этом фермент E1 влияет на скорость
функционирования двух других ферментов E2 и E3 и, соответственно, второй фермент
имеет влияние на E1 и E3, а третий - на первые два.
Допустим, имеем цепь с субстратом S, промежуточными продуктами P1, P2 и
конечным продуктом P3. Напишем реакции цепи по отдельности:
|
| S + E1 |
K21
|
E1S |
K41
|
P1 + E1
(при этом E1 влияет на
формирование P2 и P3) ,
| |
|
| P1 + E2 |
K22
|
E2P1 |
K42
|
P2 + E2
(E2 имеет влияние на формирование P1 и P3) ,
| |
|
| P2 + E3 |
K23
|
E3P3 |
K43
|
P3 + E3
(E2 имеет влияние на
формирование P1 и P2) .
| | |
| |
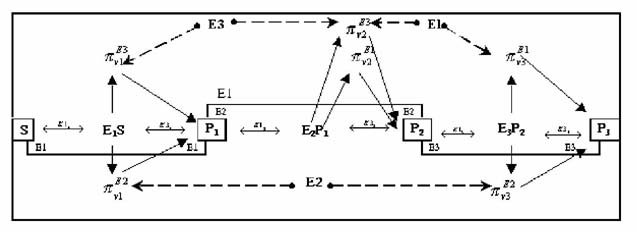
Три пары параметров гибкости, характеризующие воздействия ферментов,
схематически показаны на рис. 1.
Рис. 1. Схема воздействия параметров гибкости на
локальные скорости реакций
в трехферментной цепи с тремя ферментами в комплексе.
Рассмотрим формирование значений
одной пары параметров - параметра
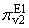 и параметра
и параметра
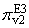 , которые зависят от концентраций
соответственно первого и третьего свободного фермента (E1 и E3) в данный момент
реакции и от скорости образования фермент-субстратного комплекса E2P1 второй
реакции цепи. Согласно формуле (1), параметры определяются следующими
формулами:
, которые зависят от концентраций
соответственно первого и третьего свободного фермента (E1 и E3) в данный момент
реакции и от скорости образования фермент-субстратного комплекса E2P1 второй
реакции цепи. Согласно формуле (1), параметры определяются следующими
формулами:
|
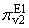 = (ln rate1 E2P1)ў / (ln E1)ў , = (ln rate1 E2P1)ў / (ln E1)ў ,
| |
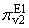 = (ln rate E2P1)ў / (ln E3)ў . = (ln rate E2P1)ў / (ln E3)ў . | | |
| |
(1) |
Оба
параметра гибкости прибавляются к значению константы скорости K32 и
таким образом участвуют в образовании второго промежуточного продукта P2:
|
rate
P2 =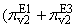 + K32)*[E2P1] - K42*[P2]*[E2] . + K32)*[E2P1] - K42*[P2]*[E2] . | | |
| |
Аналогичным образом определяются остальные пары параметров гибкости,
меняя значения соответствующих констант скоростей K3. Можно заметить, что
все параметры гибкости непосредственно зависят также друг от друга.
Результаты прогонки
моделей. Вышеописанная модель была апробирована в течение 1000
условных единиц времени, с теми же начальными значениями, что и при прогонке
изолированной модели. В результате были выявлены следующие закономерности:
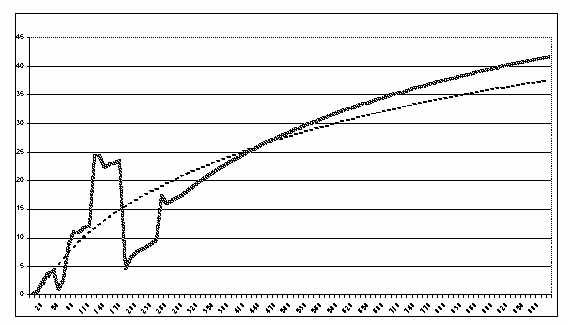
Рис. 2. Сравнительная динамика изменения концентрации первого промежуточ-
ного продукта трехферментной цепи в изолированной и комплексной моделях:
прогонка моделей в 1000 условных единицах времени (ось X - время,
ось Y - концентрация продукта, сплошная линия - комплекс E1-E2-E3,
пунктир - изолированная цепь.)
----------
1
Здесь и далее в формулах скорость обозначается словом
"rate".
1. Вплоть до 350-й условной единицы
времени наблюдаются резкие колебания в концентрации первого промежуточного
продукта P1 в комплексной цепи по сравнению с изолированной цепью
(см. рис 2). В дальнейшем динамика роста концентрации принимает
гиперболический вид (подобно динамике изолированной цепи на всем протяжении
реакции) и к 450-й условной единице времени имеет значение, равное концентрации
P1 в тот же момент времени в изолированной цепи. Следует также отметить,
что в комплексной цепи рост концентрации P1 имеет более высокий угловой
коэффициент, в результате к 1000-му условному моменту времени концентрация
продукта на 15% больше, чем в изолированной цепи.
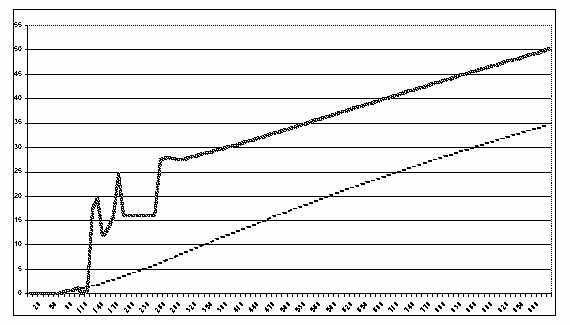
Рис. 3. Сравнительная динамика изменения концентрации второго промежуточ-
ного продукта трехферментной цепи в изолированной и комплексной моделях:
прогонка моделей в 1000 условных единицах времени (ось X - время,
ось Y - концентрация продукта, сплошная линия - комплекс E1-E2-E3,
пунктир - изолированная цепь.)
2. Концентрация второго
промежуточного продукта в комплексной цепи претерпевает резкое повышение в
период 100-120 условных единиц времени, с дальнейшими менее резкими колебаниями
вплоть до 300-й условной единицы. К этому моменту она уже в 4 раза (или на
20-22 единицы) превышает собственную концентрацию в изолированной цепи. В
дальнейшем рост концентрации принимает линейный характер, с угловым
коэффициентом, почти равным росту в изолированной цепи
(см. рис. 3). В результате к концу апробированного периода
разница значений концентраций продукта P2 составляет около 40% или 14-18 единиц.
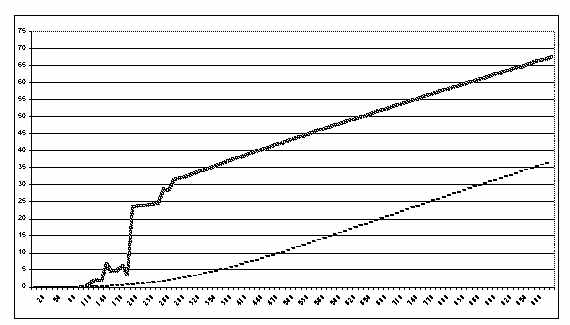
3. Динамика изменения концентраций
конечного продукта P3 похожа на описанную выше, с начальными колебаниями в
комплексной цепи и линейным характером после 300-й условной единицы
времени. В итоге к концу апробированного времени концентрация P3 в
комплексной цепи более чем в два раза превышает свое же значение в изолированной
цепи (см. рис. 4).
|
|
Рис. 4. Сравнительная динамика изменения концентрации конечного
продукта трехферментной цепи в изолированной и комплексной моделях:
прогонка моделей в 1000 условных единицах времени (ось X - время,
ось Y - концентрация продукта, сплошная линия - комплекс E1-E2-E3,
пунктир - изолированная цепь.)
В заключение следует отметить, что комплексное воздействие ферментов в
конечном итоге более результативно с точки зрения формирования конечного
продукта, определяющего общую скорость цепи, несмотря на нестабилизированные
колебания в начальной стадии реакции. Сказанное верно только для тех
ферментов, взаимное воздействие которых определяется только параметрами
гибкости, без наличия других побочных факторов изменения поведения участвующих в
цепи ферментов.
Институт молекулярной биологии НАН РА
Литература
1. Segal L. A. Mathematical Models in Molecular and Cellular Biology. N. Y., 1980.
P. 350.
2. Lam C. F. Techniques for the Analysis and Modeling of Enzyme Kinetic Mechanism.
Cambridge press. 1981. P. 265.
3. Gevorgyan A. E. - Proceedings of the CSIT Conference.
August 19-21, 1999. Yerevan, Armenia. P. 498-501.
4. Sauro H., Kacser H. - Eur. J. Biochem. 1990. V. 187. P. 493.
5. Kacser H., Sauro H., Acerenza
L. - Eur. J. Biochem. 1990. V. 187. P. 481.