а также условиям контакта на прямой у = 0.
Вначале в качестве условий контакта используем известные в строительной механике условия,
когда на линии контакта у = 0 расположены шарниры:
|
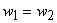 |
(1.2) |
|
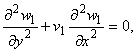 |
(1.3) |
|
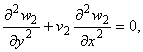 |
(1.4) |
|
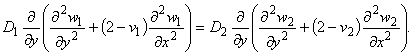 |
(1.5) |
Условия (1.3), (1.4) представляют собой равенства нулю изгибающих моментов, условие (1.5) -
равенство обобщенных перерезывающих сил контактирующих пластин. Представляя решение в виде бегущей волны с частотой
w и волновым числом k
получим следующее уравнение относительно амплитуды изгибных волн:
|
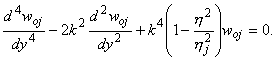 |
1.6 |
Здесь
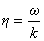 есть неизвестная фазовая скорость локализованной волны,
есть неизвестная фазовая скорость локализованной волны,
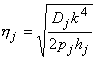 - фазовые
- фазовые
скорости одномерных изгибных волн пластин. Из общих решений уравнений (1.6) выберем только те, которым соответствует
уменьшение амплитуд при у ®
± ¥
Используем условия контакта (1.2)-(1.5) при y = 0
получим следующее дисперсионное уравнение относительно
h- неизвестной фазовой скорости локализованной волны:
|
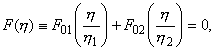 |
1.7 |
где функция
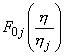 имеет вид
имеет вид
Функция
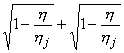 в интервале h Î [0,
min(h1, h2)]
является монотонно убывающей и,
в интервале h Î [0,
min(h1, h2)]
является монотонно убывающей и,
следовательно, в этом же интервале функция
F(h) является монотонно возрастающей.
В левом конце интервала h = 0 имеем
|
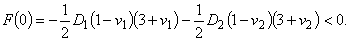 |
1.8 |
Так как функция
F(h) является монотонно возрастающей, из условия (1.8) имеем, что для
существования корня дисперсионного уравнения (1.7) необходимо и достаточно, чтобы
|
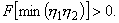 |
1.9 |
Таким образом, при выполнении неравенства (1.9) мы имеем случай
существования одной-единственной локализованной изгибной волны с фазовой скоростью
0 < h < min (h1, h2). В случае одинаковых
материалов мы получим уравнение, совпадающее с уравнением для пластинки со свободным краем [2,3].
Пусть
Тогда условие существования локализованной изгибной волны имеет вид
При b<<1 имеем, в частности, следующее условие:
2. Рассмотрим теперь эту задачу при условиях полного упругого контакта.
В этом случае условия на прямой у = 0 имеют вид:
|
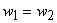 |
2.1 |
|
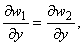 |
2.2 |
|
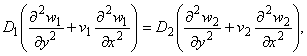 |
2.3 |
|
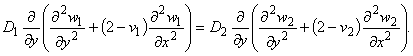 |
2.4 |
Здесь условие (2.3) представляет собой равенство изгибных моментов контактирующих
пластин, условие (2.4) - равенство обобщенных перерезывающих сил контактирующих пластин.
В [5] была исследована аналогичная задача, однако в этой работе
вместо условия равенства обобщенных перерезывающих сил контактирующих пластин было использовано
неточное условие равенства перерезывающих сил.
Повторяя предыдущий ход решения, для фазовой скорости
локализованной изгибной волны получим следующее дисперсионное уравнение:
|
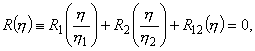 |
2.5 |
где
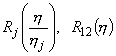 есть следующие функции:
есть следующие функции:
В точке
h = 0 имеем
Функции
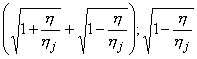 - монотонно убывающие функции в интервале h Î [0,
- монотонно убывающие функции в интервале h Î [0,
min(h1, h2)],
и, следовательно,
в этом же интервале функция R(h) является монотонно возрастающей функцией.
Таким образом, условие R[min(h1,h2)]
> 0 будет являться необходимым и
достаточным условием существования локализованной изгибной волны.
Институт механики НАН РА
Литература
1. Stonely R. - Proc. Roy. Soc. London. 1924. V. 106. P. 416-429.
2. Коненков К.Ю. - Акуст. журн. 1960. Т. 6. № 1. С. 124-126.
3. Амбарцумян С.А., Белубекян М.В. - ПМ. Т. 30(40). №2, С. 61-68(1994)
4. Багдасарян Р.А., Казарян К.Б. - ДАН АрмССР. 1986. Т. 83. № 2. С. 69-72.
5. Зильберглейт А.С., Суслова И.Б. В сб.:
Исследования по механике твердого деформируемого тела. Ереван: Изд-во АН Армении, 1981. С. 128-133.
![]()
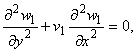
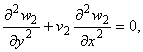
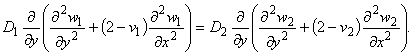
![]()
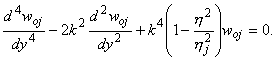
![]() есть неизвестная фазовая скорость локализованной волны,
есть неизвестная фазовая скорость локализованной волны,
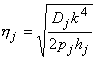 - фазовые
- фазовые 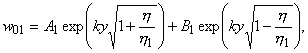
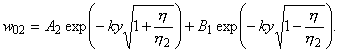
![]()
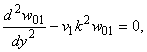
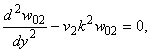
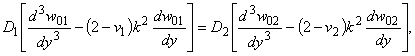
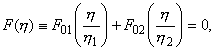
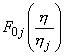 имеет вид
имеет вид
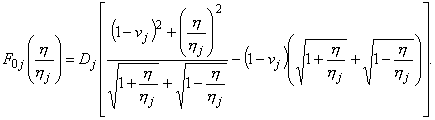
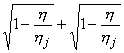 в интервале h Î [0,
min(h1, h2)]
является монотонно убывающей и,
в интервале h Î [0,
min(h1, h2)]
является монотонно убывающей и, ![]()
![]()
![]()
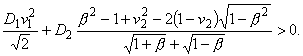
![]()
![]()
![]()
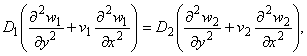
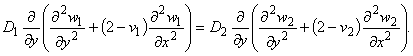
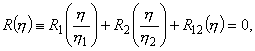
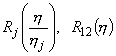 есть следующие функции:
есть следующие функции: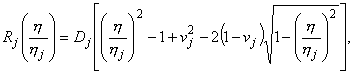
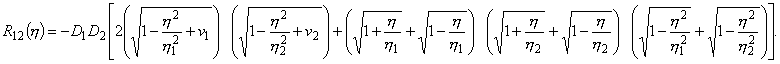
![]()
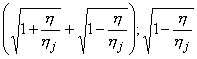 - монотонно убывающие функции в интервале h Î [0,
- монотонно убывающие функции в интервале h Î [0,