МАТЕМАТИКА
УДК 621.39.1:519.24
Э.А. Мирзаханян
О некоторых типах бесконечномерных гомотопических групп
в гильбертовом пространстве
(Представлено академиком Н.У. Аракеляном 31/III 2000)
Статья посвящена бесконечномерной алгебраической
топологии, а именно построению бесконечномерных относительных гомотопических
групп пунктированных пар подмножеств вещественного (необязательно сепарабельного)
гильбертова пространства H. В основе всех построений лежат два специальных
класса K0 М K непрерывных
подмножеств из H [1-3].
В пункте 1 даны определения допустимых
классов K0 и K, а также некоторые сведения об
отображениях, принадлежащих этим классам. Ряд основных свойств этих классов
в частности содержится в [1-6].
В пункте 2 описывается один (назовем первым)
подход к построению бесконечномерных относительных гомотопических групп
пар подмножеств из H, называемых K0 (соотв. K)
- бесконечномерными гомотопическими группами. В целях более эффективных
приложений, потребовав от сфероидов и их гомотопий удовлетворения некоторым
условиям типа компактности, также определяются так называемые K0 (соотв. K)
- бесконечномерные гомотопические группы компактного типа.
В пункте 3 в случае сепарабельности
пространства H описывается второй подход к построению бесконечномерных
гомотопических групп некомпактного типа, основанный на понятии ортонормированного
базиса пространства H. Согласно теореме 3 рассматриваемые два подхода
эквивалентны, т.е. приводят к изоморфным группам.
1. Допустимые отображения. Как уже отмечалось
в введении, во всех построениях допустимыми отображениями будут непрерывные
отображения, принадлежащие специальным классам K0 и K,
а также целому ряду классов, построенных посредством K0
и K. Зафиксируем вещественное гильбертово пространство H.
Определение 1. Пусть G - открытое
подмножество пространства H, f :
G®H
лежит классу K или является K-отображением (относительно
H),
если выполнено условие:
а) для любой точки x0 О
G и любого вещественого числа e > 0 существуют
окрестность U=U(x0,e) М G точки x0, конечномерное (линейное) подпространство
L=L(x0,e)
пространства
H и действительное число l
такие, что если точки x, y О U
и вектор (x-y) ортогонален к L,
то выполнено соотношение:
|
||f(x) - f(y) - l(x - y)|| Ј
e||x - y||. |
Далее будем говорить, что K-отображение
f : G ®
H принадлежит классу
K0 или является K0-отображением,
если выполнено:
b) (локальное удовлетворение условию Липшица)
для любой точки x0 О G
существуют такие числа r =
r(x0) и c =
c(x0),
что при x, y О G, ||x-x0||
< r, ||y-x0||
< r выполнено соотношение
|
||f(x) - f(y)|| Ј
c||x - y||. |
Фигурирующее в а) действительное число
l
можно выбрать так, чтобы оно определялось только точкой x0
и было пригодно для любого числа e > 0. Получающаяся
таким образом действительная функция l(x)
= lf(x),
заданная на G, непрерывна и единственна [2]; она называется терминальной
производной отображения f. Отметим, что композиция двух K0-отображений
есть K0-отображение, но композиция K-отображений
не всегда есть K-отображение.
Пусть теперь X - произвольное (необязательно
открытое) подмножество из H. Будем говорить, что непрерывное отображение
f : X ®
H является K0 (соотв. K)-отображением,
если существует открытое в H подмножество
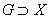 и K0
(соотв. K)-отображение
и K0
(соотв. K)-отображение
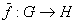 ,
такие, что
,
такие, что
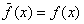 для каждой точки x О X. Если X
и Y - подмножества из H и f : X®Y
- непрерывное отображение, то f будем называть K0
(соотв. K)-отображением X в Y, если отображение f : X ® H,
т.е. композиция iof : X ® Y,
где i : Y® H - вложение,
является К0 (соотв. K)-отображением. Через
K0(M)
(соотв. K(M)) будем обозначать класс всех K0
(соотв. K)-отображений гильбертова пространства M.
для каждой точки x О X. Если X
и Y - подмножества из H и f : X®Y
- непрерывное отображение, то f будем называть K0
(соотв. K)-отображением X в Y, если отображение f : X ® H,
т.е. композиция iof : X ® Y,
где i : Y® H - вложение,
является К0 (соотв. K)-отображением. Через
K0(M)
(соотв. K(M)) будем обозначать класс всех K0
(соотв. K)-отображений гильбертова пространства M.
2. Некоторые типы бесконечномерных гомотопических
групп.
В этом пункте мы снова будем предполагать
зафиксированным действительное гильбертово пространство H. Напомним,
что (линейное) подпространство M пространства H называется
подпространством конечной коразмерности (или дефекта) q і
0, если ортогональное дополнение к M в H имеет размерность
q.
Нам, однако, понадобится ввести понятие надпространства пространства
H
коразмерности q, если q - отрицательное целое число. Именно, если q отрицательное целое число, то гильбертово
пространство M мы будем называть по отношению к H надпространством
коразмерности q, если M содержит H в качестве своего
подпространства коразмерности q.
Условимся через B(M),
B*(M)
и S(M) обозначать соответственно единичные замкнутый, открытый
шары и единичную сферу подпространства или надпространства M пространства
H.
Дадим теперь определение класса K*q,
q
О Z. При q=0 мы определим
K*0
как множество всех отображений j : H ® H,
принадлежащих классу K0(H). Если q > 0,
то под K*q
мы будем понимать множество всех отображений j : M ® H,
принадлежащих классу K0(H), где M М
H - подпространство коразмерности q. Наконец, при q
< 0 под К*q
мы будем понимать множество всех отображений j :
M ®
H, принадлежащих классу K0 относительно гильбертова пространства M,
являющегося надпространством коразмерности
q пространства H.
Пусть теперь M некоторое зафиксированное
подпространство или надпространство конечной коразмерности q О Z
пространства H. Выберем некоторый единичный вектор e О
M и обозначим через Me подространство M,
ортогональное к прямой Le, проходящей через e.
Далее положим
|
Je(M) = {x О M;
(x,e)
і 0, x П
Le x B*(M)}И{xО
M\B*(M)); (x,e)
Ј 0} |
(1) |
Пусть (X,A,x0)
тройка, состоящая из произвольного множества X М
H,
его подмножества A М X и точки
x0 О A.
Определение 2. Отображение j
: (M,M\B*(M),
Je(M))®
(X,A,x0), принадлежащее классу K*q,
будем называть (относительным) K0-сфероидом коразмерности
q
О Z пары
(X, A) в точке x0 или тройки (X,A,x0).
Обозначим через FM,eq(X,A,x0)
множество всех K0-сфероидов коразмерности q тройки
(X,A,x0) и в нем введем операцию сложения.
Выберем некоторый единичный вектор a
О
Me и для j,y
О
FM,eq(X,A,x0)
положим
| h(x)= |
м
н
о |
| j(2x
+ a),
при (x, a) Ј
0 |
|
| y(2x
- a),
при (x, a) і
0 |
|
|
|
|
(2) |
Так как отображения x®
2x + a и x® 2x
- a
принадлежат классу K0, то h О
FM,eq(X,A,x0);
K0-сфероид
h будем называть суммой сфероидов j и
y и обозначать h =
j +
y.
Определим теперь понятие гомотопности в
FM,eq(X,A,x0).
Обозначим через R числовую прямую, а I - отрезок [0,1]. Декартово
произведение M¢ =
R x
M можно рассматривать
как гильбертово пространство, для которого M является подпространством
коразмерности I. В случае q > 0 следует
за R принять любую содержащуюся в H прямую, проходящую через
нулевую точку 0 и ортогональную к M М
H.
Определение 3. Сфероиды j,y
О
FM,eq(X,A,x0)
будем называть K0-
гомотопными и записывать j
@y,
если существует отображение
F :
I x
M ® X, обладающее
свойствами:
1) F
принадлежит классу K0
относительно гильбертово пространства M¢
И H;
2)
для любого t О I
отображение
jt :
M ® X,
определяемое равенством jt(x)
= F(t; x),
x О M,
принадлежит
множеству FM,eq(X,A,x0);
3)
j0 = j
и j1
= y.
При этом отображение
F,
а также семейство (jt)
будем называть K0- гомотопией сфероидов, соединяющей j
и y. Ясно, что определяемое так понятие гомотопности
является отношением эквивалентности, только в данном случае нужно каждый
раз показать принадлежность отображений к классу K0.
Множество всех получаемых гомотопических классов будем обозначать через
PM,eq(X,A,x0).
Введенная выше операция сложения сфероидов порождает сложение гомотопических
классов по представителям в множестве PM,eq(X,A,x0)
по формуле [j]+[y]=[j+y].
Можно показать, что это сложение определено корректно, т.е. из (j
~ jў) и (y ~ yў) следует, что (j+y)
~ (jў+yў).
В самом деле, соответствующую K0-гомотопию получим, положив:
Теорема 1. При любом целом q множество
PM,eq(X,A,x0)
относительно операции сложения [j]+[y]
= [j+y]
является коммутативной группой.
Построенная группа обозначается через PM,e,aq(X,A,x0).
В построении группы PM,e,aq(X,A,x0)
участвуют три элемента выбора, а именно подпространство или надпространство
M
коразмерности q пространства H, единичный вектор
e
О M и единичный вектор e О
Me. Из нижеследующих трех предложений следует независимость
этой группы от элементов выбора.
Предложение 1.
При любом
целом q группы PM,e,aq(X,A,x0)
и PM,e,aўq(X,A,x0),
построенные посредством различных единичных векторов a,aўО
Me, изоморфны между собой.
В силу предложения 1 запись PM,e,aq(X,A,x0)
можно сократить до PM,eq(X,A,x0).
Предложение 2. При любом целом q
группы PM,eq(X,A,x0)
и PM,e1q(X,A,x0),
построенные посредством различных единичных векторов e,eўО
M, изоморфны.
В силу предложения 2 можно обозначение PM,eq(X,A,x0)
сократить до PMq(X,A,x0).
Предложение 3. Пусть M1
и M2 два различных подпространства или надпространства
одной и той же коразмерности q О Z
пространства H. Тогда группы PM1q(X,A,x0)
и PM2(X,A,x0)
изоморфны между собой.
Таким образом, при q О Z
с точностью до изоморфизма группы PMq(X,A,x0)
не зависит от выбора M, и мы можем в обозначении букву M
опускать и обозначать через Pq(X,A,x0).
Построенную группу Pq(X,A,x0)
будем называть бесконечномерной (относительной) K0- гомотопической группой (некомпактного типа) коразмерности q О
Z множества
X в точке x0
относительно подмножества A или пары (x,a) в точке
x0. В случае A = {x0} она называется
(абсолютной) K0-гомотопической группой коразмерности q
множества X в точке x0 и обозначается через Pq(X,A,x0).
В последнем случае K0-сфероиды суть K0-отображения j
: (М,М
\ B(M))
® (X,x0).
Перейдем теперь к определению бесконечномерных
K0-гомотопических
групп компактного типа.
Определение 4. K0-сфероид
j : (М,М
\ B*(M)),
Je(М))
®
(X,A,x0) коразмерности q О
Z пары (X,A) точки x0
будем называть K0-сфероидом компактного типа, короче
Kс0-сфероидом, если выполнено условиe:
c) для любого компактного множества c М
(X \ { x0}) множество
j-1(c) З B(M)
компактно, и если оно не пусто, то на нем терминальная производная lj(x)
отображения j тождественно отлична от нуля.
Аналогично определяются K0-гомотопия
сфероидов F : I x M ® X
компактного типа (короче Kc0-гомотопия сфероидов)
и Kc0-гомотопность двух Kc0-сфероидов.
Все описанные выше конструкции проходят
и в том случае, когда K0-сфероиды и их K0-гомотопии
заменяются Kc0-сфероидами и Kc0-гомотопиями
сфероидов соответственно. В результате строятся новые группы, которые мы
будем называть бесконечномерными K0-гомотопическими группами
компактного типа, короче Kc0-гомотопическими
группами, и обозначать через Pcq(X,A,x0).
Наконец, если в основе всех вышеприведенных
определений и конструкций вместо класса K0 положить класс
K,
то мы получим группы другого типа, которые будем называть бесконечномерными
K-гомотопическими
группами, соответственно K-гомотопическими группами компактного
типа пары (X, A) в точке x0, и обозначать
через KPq(X,A,x0)
и KPcq(X,A,x0).
Замечание 1. Для полной ясности можно было
бы группу Pq(X,A,x0)
обозначать через Pq(X,A,x0;H).
В этой связи отметим, что если гильбертово пространство H является
подпространством конечной коразмерности h і
0 пространства H*, то мы будем
иметь Pq(X,A,x0;H)
@ Pq+n(X,A,x0;H*)
при любом q О Z.
Далее, если гильбертовы пространства H1 и H2
таковы, что пространство H М H1 З H2
имеет одну и ту же конечную коразмерность относительно H1
и H2 и X М H,
то при любом q О Z
будем иметь: Pq(X,A,x0;H1) @ Pq(X,A,x0;H2).
Приведенные соотношения имеют место и для упомянутых выше гомотопических
групп других типов.
3. Случай сепарабельного гильбертова пространства.
В этом пункте рассматриваемое гильбертово пространство H сепарабельно.
Пусть s = (en) - произвольный
ортонормированный базис в H, a Sqs,
Tqs :
H ® H - линейные ограниченные операторы,
определяемые по формулам
| Sqs(en) = |
м
н
о |
|
|
| en-q, при n = q + 1, q + 2,ј |
|
|
|
|
(3) |
|
Tqs(en) =
en+q,
при n = 1,2,ј |
(4). |
Ни одно из этих отображений не принадлежат классу
K0,
но их композиции принадлежат. С помощью класса K0 построим
ряд других классов Kqs
(q - любое целое число) отображений подмножеств из H.
Определение 5. Пусть G открыто в
H,
а f : G ® H - непрерывное
отображение. Мы скажем, что f принадлежит классу Kqs
при q і 0, если его можно представить
в виде f = joTqs,
где j определено на Tqs(G)
и принадлежат классу K0(H). Далее скажем, что
f
принадлежит Kqs
при q Ј 0, если f можно представить
в виде f = S-qsoy,
где y О K0(H).
Мы сохраним некоторые обозначения пункта
2, в частности, B(H) = B, B*(H) = B*
суть единичный замкнутый и открытый шар в H, соответственно, и Je1(H) = {xО
H; (x,e1)
і
0, x П Le1 x B*(He1)} И {xО
(H\B*(H)); (x,e1)
Ј
0}. Пусть снова (X,A,x0)
- фиксированная пунктированная пара в H.
Определение
6. Отображение f : (H,H\B*, Je1(H)) ® (X,A,x0),
приндлежащее классу K(q)s,
будем называть K0-сфероидом второго рода коразмерности
q
О Z паре
(X,A) в точке x0.
Множество всех таких сфероидов обозначим
через Fs,e1q(X,A,x0)
и в нем введем операцию сложения, определив сумму f + g по
формуле
| (f + g)(x) = |
м
н
о |
| f(2x + e2),
при (x,e2) Ј
0, |
|
| g(2x - e2),
при (x,e2) і
0. |
|
|
|
|
Далее, в Fs,e12(X,A,x0)
введем отношение гомотопности. Пусть R - числовая прямая, а I
- единичный отрезок. В гильбертовом пространстве H* = R x H
рассмотрим ортонормированный базис s* = (e0,e1,e2,јenј),
где e0 = (1,0), а s = (en)
- рассматриваемый выше базис в H.
Определение 7. Сфероиды f,g О
Fs,e1q(X,A,x0)
будем называть K0-гомотопными и писать f @ g,
если существует непрерывное отображение F : I x H ® X,
обладающее следующими свойствами:
1) F принадлежит классу K(q)s*;
2) Для любого t О I
отображение ft : H ® X,
определенное равенством ft(x) = F(t,x),x О
H, принадлежит множеству Fs, e1q(X,A,x0);
3) f0 = f и f1 = g.
Отображение F, а также соответствующее
семейство ft называется K0-гомотопией
сфероидов второго рода, соединяющей f и g.
Отношение f @
g
есть отношение эквивалентности и, следовательно, Fs,eq(X,A,x0)
разбивается на классы эквивалентности (гомотопические классы), множество которых
обозначим через Psq(X,A,x0).
Оказывается, что если f ~ fў
и g ~ gў,
а (ft) и (gt) - K0-гомотопии
сфероидов, соединяющие f с fў
и g с gў соответственно, то (ft
+ gt)
будет K0-гомотопией сфероидов, соединяющей f
+ g
с fў+ gў.
Это означает, что операцию сложения сфероидов можно корректно перенести
на гомотопические классы, положив [f] +
[g] = [f
+ g].
Теорема 2. Множество Psq(X,A,x0)
K0 относительно операции сложения [f]
+ [g] =
[f + g]
образует коммутативную группу.
Группу Psq(X,A,x0)
K0
будем называть бесконечномерной K0- гомотопической группой второго рода пары (X, A) в точке
x0.
Пусть M* = Rq
x H,
{e*1,e*2,ј,e*q}
- канонический базис в евклидовом пространстве Rq.
Пусть наконец s* = (e*1,e*2,ј,
e*q,
e1,ј,enј),
где s = (e1,e2,јen,ј)
- рассматриваемый выше ортонормированный базис в H. Ясно, что s*
- ортонормированный базис в M*.
Рассмотрим линейные ограниченные операторы Sqs*,
Tqs* : M* ® M*,
определенные в базисе
s* по формулам
(3), (4).
Лемма. Для того, чтобы отображение f : H ® H
при q < 0 имело вид f = S-qs
o j, где j О K0(H),
необходимо и достаточно, чтобы f можно было представить в виде f = j*o S-qs*,
где j* О K0(M*).
Теорема 3. В случае сепарабельного гильбертова
пространства H оба подхода к построению бесконечномерных K0-относительных
гомотопических групп равносильны, т.е. при любом q О
Z
и каждой пунктированной паре (X,A,x0) из H группы Psq(X,A,x0)
и PMq(X,A,x0)
изоморфны между собой при любом выборе ортонормированного базиса s
и подпространства (соотв. надпространства) M коразмерности q
пространства H.
Следствие. При любом q О Z
группы Psq(X,A,x0)
с точностью до изоморфизма не зависят от выбора ортонормированного базиса
s
пространства H.
В случае сепарабельного гильбертова пространства
H
каждую из изоморфных групп Psq(X,A,x0)
и Pq(X,A,x0)
и Pq(X,A,x0)
будем называть бесконечномерной K0-гомотопической группой
коразмерности q О Z
пары X,A в точке x0.
Замечание 2. Как в пункте 2, строятся бесконечномерные
K0- гомотопические группы
второго рода компактного типа, а также бесконечномерные
K-гомотопические группы второго рода как некомпактного, так и
компактного типа.
Замечание 3. Теорема 3 остается справедливой
и для бесконечномерных K0-гомотопических групп второго
рода компактного типа, а также для бесконечномерных K-гомотопических
групп второго рода, как для некомпактного, так и для компактного типа.
Ереванский государственный университет
Литература
1. Болтянский В.Г. - Известия
АН АрмССР. Математика. 1974. Т. 9. № 2.
2. Мирзаханян Э.А. - Уч. зап.
ЕГУ. 1990. № 3.
3. Мирзаханян Э.А. - Уч. зап.
ЕГУ. 1991. № 1.
4. Мирзаханян Э.А., Болтянский
В.Г. - Известия АН АрмССР. Математика. 1974. Т. 9. № 5.
5. Мирзаханян Э.А. - Известия
АН АрмССР. Математика. 1980. Т. 15. № 5.
6. Мирзаханян Э.А. - Известия
АН АрмССР. Математика. 1998. Т. 33. № 6.