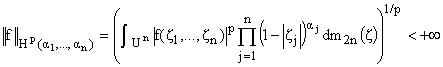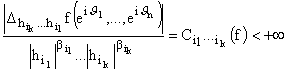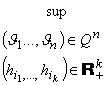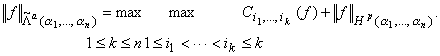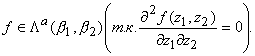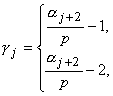Всюду ниже будем полагать, что
Zk+
- множество векторов, компоненты
которых
- натуральные числа, Rk+
- множество векторов с положительными компонентами и
b = (b1,...,bn)
(0 < bj < 1,
1 £ j
£ n). Приведем определение многомерных липшицевых классов, введенных в [б].
Определение 1.1. Измеримая,
ограниченная на Tn функция f
принадлежит классу
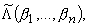 если
для любого вектора (i1,...ik)
О
Zk+
(1 £
k
£ n)
если
для любого вектора (i1,...ik)
О
Zk+
(1 £
k
£ n)
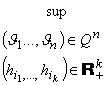
|
|
где
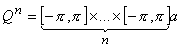 |
где
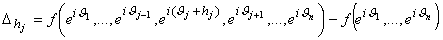
|
Далее, условимся полапать, что
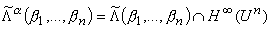 и
и |
В [б] исследованы мультипликативные свойства классов
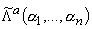 и в терминах
этих классов дано полное описание сопряженного пространства (Hp{a1,... ,an))* при 0 < р
£ 1. Там же при целозначных bj(1
£ j
£ n) дано и определение классов
и в терминах
этих классов дано полное описание сопряженного пространства (Hp{a1,... ,an))* при 0 < р
£ 1. Там же при целозначных bj(1
£ j
£ n) дано и определение классов
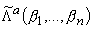 . Отметим, что классы
. Отметим, что классы
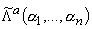 ранее были исследованы С. М. Никольским [7] в случае, когда
(hi1,..., hik) º (h1,..., hn).
ранее были исследованы С. М. Никольским [7] в случае, когда
(hi1,..., hik) º (h1,..., hn).
Определение 1.2. Оператор Теплица с символом
h О L1(Tn)
- это интегральный оператор
В дальнейшем изложении использовано также следующее определение из [8], где для удобства изменено обозначение вводимого функционального класса.
Определение 1.3. Суммируемая на
Tn функция h принадлежит классу RL, если ее коэффициенты Фурье равны нулю вне множества
Zk+
È -Zk+
.
2. Данная статья посвящена исследованию дальнейших свойств классов
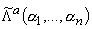 . В нижеследующих теоремах 1 и 2, соответственно, установлено,
что эти классы являются алгебрами и что они инвариантны при применении теплицевых операторов. Исходя из результатов [8], относящихся к ограниченности операторов
Th(f) в Hp{a1,... ,an), доказана теорема 3, где дано описание тех символов
. В нижеследующих теоремах 1 и 2, соответственно, установлено,
что эти классы являются алгебрами и что они инвариантны при применении теплицевых операторов. Исходя из результатов [8], относящихся к ограниченности операторов
Th(f) в Hp{a1,... ,an), доказана теорема 3, где дано описание тех символов 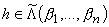 , для которых Th(f) О Hp{a1,... ,an) при любом
f О Hp{a1,... ,an). Наконец в качестве приложения теорем 2 и 3 к вопросам деления на внутреннюю функцию в пространствах
, для которых Th(f) О Hp{a1,... ,an) при любом
f О Hp{a1,... ,an). Наконец в качестве приложения теорем 2 и 3 к вопросам деления на внутреннюю функцию в пространствах 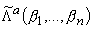 и
Hp{a1,... ,an)
(0 < р £ 1) установлена теорема 4.
и
Hp{a1,... ,an)
(0 < р £ 1) установлена теорема 4.
Теорема 2.1. Классы
La = (b1,...,bn) являются алгебрами.
Замечание.
Классы
La = (b1,...,bn) в
отличие от 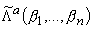 , доказанным свойством не обладают. При этом
существуют такие f, g О
La = (b1,...,bn), что
f · g Ï
La = (b1,...,bn).
Действительно, пусть n = 2 и g(z) = z1 · z2. Если
f(z1, z2) = j(z1) +
j(z2), где j1,
2
произвольные дифференцируемые функции, то, очевидно,
, доказанным свойством не обладают. При этом
существуют такие f, g О
La = (b1,...,bn), что
f · g Ï
La = (b1,...,bn).
Действительно, пусть n = 2 и g(z) = z1 · z2. Если
f(z1, z2) = j(z1) +
j(z2), где j1,
2
произвольные дифференцируемые функции, то, очевидно,
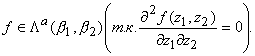 Однако ясно, что f
· g О
La = (b1,...,b2)
не для всех возможных j1
и j2.
Однако ясно, что f
· g О
La = (b1,...,b2)
не для всех возможных j1
и j2.
Напомним,
что функция f называется мультипликатором пространства X, если f
· g О
Х при любом g О X.
Теорема 2.2. Пусть
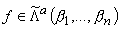 - любая
функция и
- любая
функция и
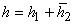 , где h1 голоморфный
мультипликатор пространства
, где h1 голоморфный
мультипликатор пространства
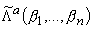 ,
а
,
а
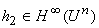 .
Тогда
.
Тогда 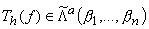 .
.
Следующая
теорема 3, доказанная на основе результатов [6] и [8], в терминах функций из
классов
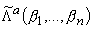 характеризует множество символов h, при которых ограничен
теплицев оператор в классах Hp(a1,...,an).
характеризует множество символов h, при которых ограничен
теплицев оператор в классах Hp(a1,...,an).
Теорема 2.3. Пусть
(0 < р £ 1) и h О RL любые. Тогда
Th(f) О Hp(a1,...,an) только в том случае, когда справедливо
представление 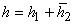 ,
где h1 О
H¥(Un), a
,
где h1 О
H¥(Un), a
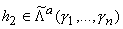 , где gj(1
£ j
£ n) определены из равенств
, где gj(1
£ j
£ n) определены из равенств
|
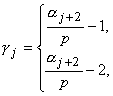
|
при нецелых aj
при целых aj |
Перейдем к приложению установленных выше результатов к вопросам деления пространствах Hp(a1,...,an)
и
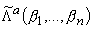 . Для этого сначала введем следующие общепринятые определения.
. Для этого сначала введем следующие общепринятые определения.
Определение 2.1. Функция g О
H¥(Un) называется внутренней, если для ее радиальных предельных значений |g*(w)| = 1 почти всюду на
Tn.
Определение 2.2.
Внутреннюю функцию g О
H¥(Un) будем называть
хорошей, если u[g] = 0, u[g]
- наименьшая n-гармоническая мажоранта
функции log[g] в Un ([9]) .
Теорема 4. Пусть a
= (a1,...,an), b
= (b1,...,bn),
aj > -1 и 1
£ j £ n, 0 < bj< 1, 1
£ j £ n) и X обозначает какой-либо из классов
Hp(a1,...,an)
и 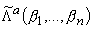 . Далее, пусть f О
X, J
- хорошая внутренняя функция, F
О H¥(Un)
и f = F · J. Тогда F
О X.
. Далее, пусть f О
X, J
- хорошая внутренняя функция, F
О H¥(Un)
и f = F · J. Тогда F
О X.
Ереванский государственный университет
Литература
1. Коренблюм Б. И. - Мат. заметки. 1971. Т. 10. № 1. С. 53-68.
2. Хавин В. П. - Зап. научн. семинаров ЛОМИ. 1971. Т. 22. С. 202-205.
3. Шамоян Ф. А. - Зап. научн. семинаров ЛОМИ. 1971. Т. 22. С. 206-208.
4. Джрбашян М. М. - ДАН Арм. ССР. 1945. Т. 3. № 1. С. 3-9.
5. Джрбашян М. М. - Сообщ. Ин-та математики и механики АН Арм. ССР. 1948. Вып. 2, С. 3-40.
6. Шамоян Ф. А., Арутюнян А. В. - Изв. НАН Армении, Математика. 1993. Т. 28. № 6. С. 50-68.
7. Никольский С. М. - Аппроксимация функций многих переменных и теоремы вложения. М.: Наука, 1969.
8. Шамоян Ф. Л., Арутюнян А. В. - Изв. НАН Армении. Математика. 1995. Т. 30. № 2. С. 70-78.
9. Рудин У. - Теория функций в полидиске. М.: Мир. 1974.