УДК 621.39.1:519.34

   В работе доказывается, что существуют тавтологии (твт) длины n, для которых и в системах Фреге Б, и в системах Фреге с подстановками SБ оценки количества формул и общей длины выводов имеют порядок n и n² соответственно.

   1. Введение. В работах [1] и [2] обсуждается вопрос получения нижних оценок количества шагов выводов в систeмах Фреге с подстановками. В частности, Басс [1] указывает в качестве открытой проблему получения суперлогаритмической нижней оценки количества шагов выводов в SБ. Ургарт в [2] доказал, что существуют формулы с длиной O(n), количество шагов выводов которых в SБ не менее O(n / logn). Однако еще в 1981 г. в качестве некоего вспомогательного результата нами была получена линейная нижняя оценка для количества шагов выводов в классической, интуиционистской и минимальной системах с простыми подстановками исчисления высказываний гильбертовского типа [3]. Эти оценки были получены с использованием введенного в [4] понятия t-множества, непосредственное применение которого в системах Фреге представляется затруднительным. В настоящей работе для произвольной твт вводится понятие множества существенных подформул, и на его основе доказывается существование последовательности формул длины n, для которых в обеих системах Б и SБ количество шагов и длина выводов оцениваются соответственно функциями порядка n и n² соответственно.

    2. Основные понятия и определения. Напомним общепринятые понятия систем Фреге, выводов в них и сложностных характеристик выводов.
   Каждая система Фреге Б использует некоторое конечное, функционально полное множество пропозициональных связок. Б определяется конечным множеством схематически заданных правил вывода [(A₁ A₂ јA_k)/(B)] (при k=0 соответствующее правило определяет схему ксиом). Б непротиворечива, т. е. для каждого правила вывода, если при некотором истинностном значении переменных все A_i(1 Ј i Ј k) принимают значение "истина", то и B принимает значение "истина". Б полна, т. е. всякая тавтология выводима в Б. Система Фреге с подстановкой SБ получается из Б добавлением правила простой подстановки [(A)/(As)], где s - отображение, ставящее в соответствие переменной формулы A некоторую формулу (в частности переменную), и As - результат повсеместной замены этой переменной в A на соответствующую формулу.
   В дальнейшем мы будем считать зафиксированными некоторую систему Фреге Б и соответствующую систему с подстановкой SБ. Результат настоящей работы не зависит от выбора системы, однако для упрощения рассматриваемого примера мы будем предполагать, что в числе прочих язык Б содержит логические связки ® и Щ.
   Мы будем пользоваться общепринятым определением вывода в данной системе как последовательности формул, каждая из которых является аксиомой данной системы или получается из предыдущих по одному из правил вывода данной системы. Вывод в системе Б будем называть Б-выводом, а в системе SБ - соответственно SБ-выводом.
   Длину формулы F, понимаемую как количество всех символов в F, будем обозначать через (F).
   В качестве сложности вывода зафиксируем два понятия: количество различных формул (шагов) в выводе и суммарную длину всех формул вывода.
   Через Sf(F) обозначим множество всех неэлементарных подформул формулы F. Для каждой формулы F, каждой подформулы j ОSf(F) и произвольной переменной p через (F)^p_j обозначим результат повсеместной замены в F подформулы j на переменную p. При этом если j ПSf(F), то (F)^p_j=F.
   Множество различных переменных формулы F обозначим через Var(F).

   Определение. Пусть для некоторой твт F p - некоторая переменная такая, что p П Var(F) и j О Sf(F). Подформулу j назовем существенной для F, если (F)^p_j не является тавтологией.
   Множество существенных для твт F подформул обозначим через Essf(F).
   Очевидно, что если F является минимальной твт, т. е. не может быть получена подстановкой из более короткой твт, то Essf(F)=Sf(F).
   Если формулы не могут быть получены по правилу подстановки из одной и той же существенной подформулы некоторой твт, то будем говорить, что эти формулы несравнимы.
   Для каждого правила вывода [(A₁A₂ јA_k)/(B)] (k і 1) определяющей назовем любую из существенных подформул формулы A₁Щ(A₂Щ(јЩ(A_k-1ЩA_k)ј))®B. Множество определяющих подформул будем обозначать через Dsf(A₁, A₂, ј, A_k, B).
   Формулу j назовем важной в Б-выводе (SБ-выводе), если j или является существенной для некоторой аксиомы этого вывода, или является определяющей для некоторого Б-правила, примененного в выводе.^*

   3. Основные результаты. Здесь будет описан класс формул длины n, нижние оценки количества шагов и длины выводов которых имеют порядок n и n² соответственно и в Б и в SБ. В основе доказательства этого результата лежит следующее свойство существенных подформул.
   Лемма. 1)   Для   каждого  Б-правила     [(A₁A₂ јA_k)/(B)]    (k і 1)     Essf(B) Н Н

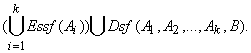
                      2) Для правила подстановки [(A)/(As)]  Essf(As) Н { js/j О Essf(A)} .

    Доказательство пункта 1) основано на непротиворечивости Б-правил.

   Доказательство пункта 2) следует из того, что если для некоторых p, j, A и s  является твт, то также твт, а значит если не является твт, то также не твт.

   Следствие. Пусть F - некоторая твт и j О Essf(F), тогда
   1) в каждом Б-выводе формулы F формула j должна быть важной;
   2) если правилами подстановки, использованными в некотором SБ-выводе формулы F, являются [(A₁)/(A₁s₁)], [(A₂)/(A₂ s₂)],ј,[(A_m)/(A_ms_m)], то j должна быть или важной формулой этого вывода, или результатом последовательных подстановок s_i1, s_i2,ј,s_iS для 1 Ј i₁, i₂,јi_S Ј m в одну из важных формул.

   Доказательство очевидным образом следует из утверждения леммы.
 

   Теорема 1. Для достаточно больших n, если F_n твт такая, что |F_n|=O(n) и для некоторого l=O(n) существуют подформулы j₁, j₂, ј, j_l такие, что
   a) { j₁, j₂, ј, j_l } О Essf(F_n),
   б) формулы j_i и j_j  (1 Ј i < j Ј l) попарно несравнимы,
   в) |j₁| < |j₂| < ј < |j_l| и |j_l|=O(n),
то количество шагов в любом Б-выводе (SБ-выводе) формулы F_n не менее, чем O(n), а длина любого Б-вывода (SБ-вывода) не менее O(n²).

   Доказательство следует из вышеприведенных утверждений и того факта, что и количество существенных подформул каждой аксиомы, и количество определяющих подформул каждого Б-правила ограничено некоторой константой.

   Пример. Нетрудно  видеть,  что  условия  теоремы  выполнены  для
F_n = (p₁ ® p₁) Щ ((p₂ ® p₂) Щ (јЩ ((p_n-1 ® p_n-1) Щ (p_n ® p_n))ј)), где j_i = (p_n-i ®
®  p_n-i) Щ ((p_n-i+1 ® p_n-i+1) Щ (јЩ (p_n-1 ® p_n-1) Щ (p_n ® p_n))ј))     (0 Ј i Ј n - 1).

   Теорема 2. Для достаточно больших n существуют формулы F_n такие, что минимальные количества шагов их Б-выводов и SБ-выводов имеют порядок n, а минимальные длины их Б-выводов и SБ-выводов имеют порядок n².
   В качестве таковых могут быть рассмотрены, например, вышеприведенные. Для них нетрудно получить одинаковые верхние оценки сложностей Б-выводов и SБ-выводов, равные по порядку нижним для обоих критериев сложностей.
   Фактически для класса формул, удовлетворяющего условиям теоремы 1, не имеет место "ускорение" выводов при переходе от Б систем к SБ системам, исследованное в работах [1, 3, 4].
   Заметим, что при мультипликативной подстановке формула F_n может быть выведена за log₂n шагов, что указывает на существенное различие способов подстановки.
   Автор благодарен участникам семинара под руководством И. Заславского за полезные советы.

   Ереванский государственный университет

     1. Buss S. R. - Arch. Math. Logic. 1995. V. 34. P. 377-394.
     2. Urquhart A. - Arch. Math. Logic. 1997. V. 37. P. 15-19.
     3. Чубарян А. А. - Прикл. математика. ЕГУ. 1981. N 1. С. 81-89.
     4. Г. С. Цейтин, Чубарян А. А. - Мат. вопр. кибернетики и вычисл. техники. Ереван: Изд-во АН АрмССР. 1975. С. 57-64.