МАТЕМАТИКА
УДК 616.8
С. Л. Амбарян
Решение уравнения Пелля
при помощи последовательностей Фарея
(Представлено академиком Ю. Г. Шукуряном 4/V 2000)
Рассмотрим диофантово (неопределенное) уравнение
2-й степени
| |
|
|
| z = F(x, y) = x2 - Dy2 -
1 = 0
, |
|
|
|
|
(1) |
где D > 0, D - неполный квадрат, которое называется
уравнением Пелля (точнее уравнением Ферма) [1,2]. Те значения x
и y, которые образуют целочисленное решение уравнения Пелля, представляют
собой соответственно числитель и знаменатель одной из подходящих дробей
к
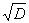 . Литературу по решению частных случаев
уравнения Пелля см. в [3]. В [4] описан алгоритм разложения квадратичной
иррациональности в непрерывную дробь, для работы которого достаточно знать
D
и целую часть
. Литературу по решению частных случаев
уравнения Пелля см. в [3]. В [4] описан алгоритм разложения квадратичной
иррациональности в непрерывную дробь, для работы которого достаточно знать
D
и целую часть
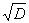 .
.
Уравнение (1) имеет бесконечное число решений
[1,2].
Пусть
| |
d = [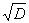 ]
, d2 < D < (d+1)2
; ]
, d2 < D < (d+1)2
; |
|
|
|
|
обозначим через D1=D-d2
, D2=(d+1)2-D
, c=2(D2-
D1)-1 ,
d =
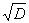 -d
, 0 < d < 1 . -d
, 0 < d < 1 . |
Представим 2d и 2(d+1) равенствами
вида
| |
| 2d = n
D1 + r1 , 0 Ј r1
< D1 ; |
|
| 2(d + 1) = mD2 + r2
, 0 Ј r2 <
D2
. |
|
|
|
|
Рассмотрим случай, когда r1 = 0,
ищем решение уравнения Пелля в виде x=a+db и y=b,
получим
это уравнение превращается в тождество при a=1 и b=n,
т. е.
Таким образом, при r1=0 либо
r2=0
решения уравнения Пелля известны, в частности, получим следующие решения
уравнения (1):
| 1. |
D1 = 1 , |
D = d2 + 1 , |
x = 2d2 + 1 , |
y = 2d ; |
| 2. |
D1 = 2 , |
D = d2 + 2 , |
x = d2 + 1 , |
y = d ; |
| 3. |
D1 = d/2
, |
D = d2 + d/2 , |
x = 4d + 1 , |
y = 4 ; |
| 4. |
D1 = d
, |
D = d2 + d , |
x = 2d + 1 , |
y = 2 ; |
| 5. |
D2 = d + 1
, |
D = (d + 1)2 - (d + 1)
, |
x = 2d + 1 , |
y = 2 ; |
| 6. |
D2 = (d + 1)/2
, |
D = (d + 1)2 - (d + 1)/2
, |
x = 4d - 1 , |
y = 4 ; |
| 7. |
D2 = 2 , |
D = (d + 1)2 - 2 , |
x = (d + 1)2 - 1 , |
y = d + 1 ; |
| 8. |
D2 = 1 , |
D = (d + 1)2 - 1 , |
x = d + 1 , |
y = 1 ; |
С помощью данной структуры представления числа
|
| D = d2 + D1 = (d + 1)2 - D2 = ((D1 -
D2 + 1)/2)2 + D1D2
= |
|
| = ((3D1 - D2 + 1)/2)2 + cD1 = ((3D2 -
D1 - 1)/2)2 - cD2
, т. е. D є f(D1,
D2)
, |
|
|
|
|
получено много интересных результатов по решению уравнения
(1). Например, пусть
(D1 + D2)
кратно 3 и D = d2 + d + 1, тогда x = (D1 + D2)y/2 + 1
и y = 4(D1 + D2)/3
или же (D1 + D2)
кратно 5 и D = d2 + d - 1,
тогда x = (D1 + D2)y/2 - 1
и y = 4(D1 + D2)/5.
Согласно приведенной таблице, в дальнейшем
предположим, что D1, D2ПП
{ 1, 2}.
Поставим следующую задачу. Найти минимальное
решение уравнения (1), отличное от тривиального решения x=1 и y=0,
при помощи последовательностей Фарея [2].
Определение 1. Последовательностью Фарея
Fn
называется множество несократимых рациональных чисел
a/b
со знаменателями bЈn, принадлежащих
сегменту [0,1] и расположенных в порядке их возрастания.
Очевидно, что
| |
d + D1 / (D1 + D2)
<
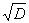 < d + D1 / (D1 + D2 - 1)
, < d + D1 / (D1 + D2 - 1)
, |
|
| 1 / (n + (r1 + 1) / D1)
< d < 1 / (n + r1 / D1)
, |
|
| 0 < 1 / (n + 1) < d
< 1 / n Ј 1) . |
|
|
|
|
(2) |
Дроби 1/(n+1) и 1/n являются соседними
дробями Фарея со знаменателем t, удовлетворяющим
условию n+1 Ј tЈ
2n+1. Отметим, что соседние элементы последовательностей
| xn = 1/n и
yn = (n - 1)/n;
n = 1, 2, 3, ј |
|
являются соседними фареевыми дробями в соответствующих последовательностях
Фарея.
Согласно теории фареевых дробей, если a/b
< x/y < p/q - три последовательные дроби
Фарея в Fn, то x/y=(a+p)/(b+q).
Дробь x/y называется медиантой дробей a/b и
p/q.
Сопоставим дроби a/b значение
функции z=F(x, y) в точке x=a+db,
y=b и введем функцию одной переменной f(x/y),
такую, что f(a/b)=(a +db)2-Db2-1,
где a/b - фареева дробь.
Определение 2. Последовательность вложенных
один в другой (каждый последующий содержится в предыдущем) промежутков
| Ek = [ak/bk,
pk/qk]
, EkЙEk+1
; k=1, 2, 3,
ј , |
|
где a1/b1 < p1/q1
соседние дроби Фарея, называется фареево-подходящей, если в качестве последующего
левого или правого конца промежутка выступает медианта концов предыдущего
промежутка.
В этих обозначениях имеет место следующая
теорема (аналог теоремы Коши).
Теорема. Пусть функция f(x/y)
на концах промежутка [a1/b1, p1/q1]
принимает значения разных знаков, тогда на множестве фареево-подходящих
последовательностей существует такая последовательность, для которой f(ak/bk)=0;
1 Ј k << Ґ.
Ниже приводится алгоритм, который находит
корни функции f(x/y).
Пусть функция f(x/y)
на концах промежутка [a1/b1, p1/q1],
которые являются соседними дробями Фарея, прнимает значения разных знаков.
Построим фареево-подходящую последовательность по следующему принципу:
а. вычислить значение функции f(x/y)
в точке a/b, равной медианте концов промежутка [a1/b1,
p1/q1];
b. если f(a/b) > 0,
то в качестве нового правого конца промежутка взять дробь a/b;
с. если f(a/b) <
0, то в качестве нового левого конца промежутка взять дробь a/b.
Процесс продолжить до тех пор, пока f(a/b)
№
0, в противном случае
является решением уравнения Пелля.
Проиллюстрируем последний шаг работы алгоритма:
| |
x = y1 + dy ,
тогда
x12 - Dy12 = -D1
и x1 / y1
<
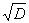 ; ; |
|
x = -y2 + (d + 1)y
, тогда x22 - Dy22 = +D2
и x2 / y2
>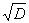 . . |
|
|
|
|
Очевидно, что x=y1+d(y1+y2)=x1+x2
, y=y1+y2 . В этих обозначениях
справедливы следующие соотношения:
| |
|
|
| |D2y1 -
D1y2|(y1 + y2) - y1y2 = 1
, |
|
| |D2x1 - D1x2|(x1 + x2) - x1x2 = -D
, |
|
| x1x2 - Dy1y2 = (D1 -
D2 + 1)/2
. |
|
|
|
|
Таким образом,
| |
x1 / y1 <
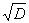 < x2 / y2 , < x2 / y2 , |
|
| (x1 - dy1) / y1
< d < (x2 - dy2) / y2
, |
|
| (y1 - |D2y1 -
D1y2|) / y1
< d < |D2y1 - D1y2| / y2
. |
|
|
|
|
Медиантой дробей границ числа d
будет y1 / (y1+y2),
т. е.
| x = y1 + d(y1 + y2),
y = y1 + y2 - решение
уравнения Пелля. |
|
Описанный алгоритм успешно решает также диофантово
уравнение 1-й степени a x+by=c и может быть
применен к решению многих задач, связанных с подходящими и/или фареевыми
дробями.
Как следствие отметим, что этот алгоритм
позволяет вычислить значение
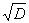 с любой
точностью.
с любой
точностью.
Существует множество значений функции f(x/y),
для которых работу построения новых медиант можно приостановить, например:
| x2 - Dy2 = {
ј,
- D1D2,
- D1,
-2,
-1,
+2, c, D2,
D12,
D22,
ј}
. |
|
Диофантово уравнение
имеет тривиальное решение x = D1 + d(D1 + D2)
и y = (D1 + D2).
При больших значениях D следует применить
арифметику многократной точности [4]. С этой целью разработан пакет прикладных
программ (ППП) выполнения арифметических операций с произвольно высокой
точностью [5]. Несмотря на то, что граничные значения D1
и D2 не рассматриваются, при больших
значениях D оценки (2) могут быть не лучшими.
Ставим задачу улучшения оценок (2):
1. найти максмальное целое число m,
для которого
| |
| m / (m + 1) Ј
D1 / (D1 + D2)
, т. е. m = [D1 / D2]
; |
|
|
|
|
2. найти минимальное целое число n, для
которого
| |
| D1 / (D1 + D2 - 1)
Ј n / (n + 1)
, т. е. n = ]D1 / (D2 - 1)[
. |
|
|
|
|
Таким образом,
| |
| m / (m + 1) < d
< n / (n + 1) . |
|
|
|
|
(2a) |
Дальнейшее улучшение оценки (2a) связано
с модификацией алгоритма нахождения нуля функции z=F(x,
y),
например, при помощи построения специальных соседних фареевых дробей либо
обычного метода деления отрезка на множестве фареевых дробей.
В заключение отметим, что описанный алгоритм
нахождения решения уравнения Пелля по количеству шагов его работы (построение
медиант), без улучшения оценок, часто уступает классическому алгоритму
нахождения решения уравнения Пелля по подходящим дробям к
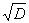 ,
которые оказались подмножеством построенных медиант.
,
которые оказались подмножеством построенных медиант.
Ереванский научно-исследовательский
институт математических машин
Литература
1. Арнольд И. В. Теория
чисел. М.: Учпедгиз, 1939.
2. Бухштаб А. А. Теория
чисел. М.: Просвещение, 1966.
3. Айерлэнд К., Роузен. М.
Классическое введение в современную теорию чисел. М.: Мир, 1987.
4. Кнут Д. Искусство программирования
для ЭВМ. Получисленные алгоритмы. М.: Мир, 1977.
5. Амбарян С. Л. В сб.:
ППП в среде Visual С++ (Windows 95). ЕрНИИММ. Ереван. 1998.
![]() . Литературу по решению частных случаев
уравнения Пелля см. в [3]. В [4] описан алгоритм разложения квадратичной
иррациональности в непрерывную дробь, для работы которого достаточно знать
D
и целую часть
. Литературу по решению частных случаев
уравнения Пелля см. в [3]. В [4] описан алгоритм разложения квадратичной
иррациональности в непрерывную дробь, для работы которого достаточно знать
D
и целую часть
![]() .
.
![]() с любой
точностью.
с любой
точностью.
![]() ,
которые оказались подмножеством построенных медиант.
,
которые оказались подмножеством построенных медиант.