УДК 539.3

    Асимптотическим методом выведены рекуррентные формулы для определения напряженно-деформированного состояния двухслойной полосы из сжимаемого и несжимаемого слоев. Считается, что на продольных краях полосы заданы кинематические условия. Задача, в частности, моделирует работу резинометаллических сейсмоизоляторов. В качестве иллюстрации приведены решения ряда прикладных задач.
    1. Имеем двухслойную полосу W = {x, z : -h_e Ј z Ј h, -l Ј x Ј l, h+h_e << 2l}. Слой 0 Ј z Ј h - из сжимаемого материала, а слой -h_e Ј z Ј 0 - из несжимаемого. Считается, что продольным краям полосы сообщены перемещения:

ux(x, z = -he) = ux-(x),  uz(x, z = -he) = uz-(x),  ux(x, z = h) = ux+(x),   uz(x, z = h) = uz+(x),

(1.1)

а между слоями имеет место полный контакт:

szz(x, z = 0) = sezz(x,z = 0),   sxz(x, z = 0) = sexz(x, z = 0),  ux(x, z = 0) = uex(x, z = 0),   uz(x, z = 0) = uez(x, z = 0).

(1.2)

    Здесь и в дальнейшем всем величинам несжимаемого слоя приписывается индекс e.
    В общем случае считается, что на двухслойную полосу действует также температурное поле.
    Для решения задачи воспользуемся рекуррентными формулами для сжимаемого слоя [1,2]:

Q=ec S е s=0 esQ(s)(x,z),     0 Ј z Јz1  ,  cu=-1,   cs=0  ,

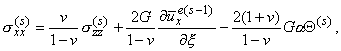
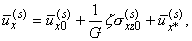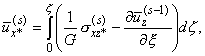
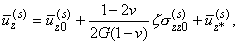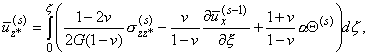
szz(s)=szz0(s)+szz*(s),    szz*(s)=- z у х 0 ¶sxz(s-1) ¶x dz ,  sxz(s)=sxz0(s)+sxz*(s),    sxz*(s)=- z у х 0 ¶sxx(s-1) ¶x dz ,                                  z1= h h+he ,     Q = e-1 S е s=0 Q(s)(x,z),

(1.3)

а для несжимаемого слоя - следующими рекуррентными формулами, по модели Дюгамеля-Неймана учитывающими влияние температурного поля:
 
 

Qe=ec S е s=0 esQe(s)(x,z),   -ze Ј z Ј 0  ,

szze(s) = szz0e(s) + szz*e(s),   szz*e(s) = - z у х 0 ¶sxze(s-2) ¶x dz ,

(1.4)

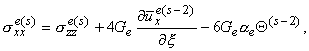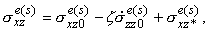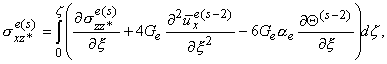
где точки над буквами означают производные соответствующих порядков по x.
    В (1.3), (1.4) неизвестными остаются величины с нулевым индексом.
    Используя формулы (1.3), (1.4) и удовлетворив условиям (1.1), (1.2), можно определить эти величины, а следовательно, решить внутреннюю задачу.
    Приведем формулы для вычисления напряжений и перемещений, соответствующие первым двум шагам итерации, обеспечивающим точность 0(e²):
    а) сжимаемый слой (0 Ј z Ј h)
   

szz=s ,     sxx= n 1-n s- 2(1+n) 1-n ha M Q ,   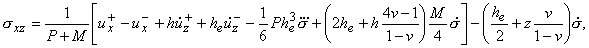  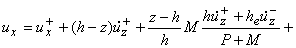          + z - h h M P+M й к л ux+- ux-- 1 6 Phe3 ј s + ж з и 2he+ h 4n-1 1-n ц ч ш M 4 . s щ ъ ы -         - z-h h he M 2 . s + M 2h n 1-n (h2-z2) . s - M(1-2n) 4h(1-n) (z-h)2 . s  ,  uz=ux++(z-h) 1-2n 2h(1-n) Ms+(z-h) 1+n 1-n aQ ,

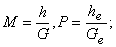(1.5)

    б) несжимаемый слой (-h_e Ј z Ј 0)  

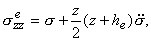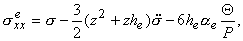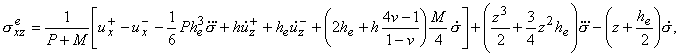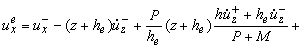
+ z+he he P P+M й к л ux+ - ux-  - Phe3 6 ј s - ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s щ ъ ы +           + P 12he (z+2he)(z3+h3e) ј s - P 2he z(z+he) . s  ,  uze = uz-+P ж з и z2-he2 4 + z3+h3e 6he ц ч ш .. s +3(z+he)aeQ,

(1.6)

где s - решение дифференциального уравнения

k2 = 6(1-2n) he2(1-n) M P  ,  W= 2(1-n) 1-2n uz+ - uz- - ж з и 3heae + ha 1+n 1-n ц ч ш Q M    ,

(1.7)

удовлетворяющее интегральным граничным условиям на торцах x = ± l полосы

h у х -hp sxx(x = ± l, z ) dz = 0  .

(1.8)

Этим решением при u_z⁺ - u_z^- = ax + b является
    

s = A ch kx chkl +B shkx shkl +W  ,  A=C й к л T-H b- ж з и 3heae+ha 1+n 1-n ц ч ш Q M   щ ъ ы  ,

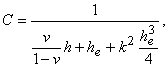
B=C(T-H al M )  ,    H= 2(1-n) 1-2n ж з и n 1-n h + he ц ч ш  ,  T= 2a(1+n)h2Q M(1-n) + 6h2eaeQ P  .

(1.9)

    2. В качестве приложения приведем решения некоторых прикладных задач.
    а) Продольным краям полосы сообщены постоянные нормальные перемещения, изменение температурного поля также постоянно:

uz± = const  ,     ux± = 0  ,     Q = const  .

(2.1)

    Подставив (2.1) в (1.5)-(1.9), получим:
  для сжимаемого слоя (0 Ј z Ј h)

szz = s ,     sxx= n 1-n s - 2(1+n) 1-n ha M Q ,  sxz= 1 P+M й к л ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - 1 6 Phe3 ј s щ ъ ы - ж з и he 2  + z n 1-n ц ч ш . s  ,  ux= z-h h M P+M й к л ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - 1 6 Phe3 ј s щ ъ ы -         - z-h h he M 2 . s + M 2h n 1-n (h2-z2) . s - M(1-2n) 4h(1-n) (z-h)2 . s  ,  uz=uz+ + (z-h) 1-2n 2h(1-n) Ms + (z-h) 1+n 1-n aQ ;

(2.2)

  для несжимаемого слоя (-h_e Ј z Ј 0)

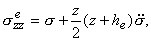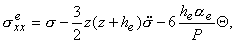sxze= 1 P+M й к л ж з и 2he+h 4n-1 1-n ц ч ш M 4 . s - 1 6 Ph3e ј s щ ъ ы +          + ж з и z3 2 + 3 4 z2he ц ч ш ј s - ж з и z+ he 2 ц ч ш . s  ,

uxe= (z+he)P he(P+M) й к л ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - P 6 he3 ј s щ ъ ы +           + P 12he (z+2he)(z3+h3e) ј s - P 2he z(z+he) . s  ,  uze=uz- + P ж з и z2-he2 4 + z3+h3e 6he ц ч ш .. s +3(z+he)aeQ.

(2.3)

Для этого случая в формуле (1.9) для s необходимо принять a = 0,  b = u_z⁺ - u_z^-.
    Деформированное состояние полосы представлено на рис. 1.

    б) Одной из продольных сторон полосы сообщены нормальные перемещения, меняющиеся линейно по длине балки, изменение температурного поля постоянно:
 

uz- = 0  ,     uz+ = ax+b  ,     ux±  = 0  ,     Q = const  .

(2.4)

    Компоненты s_zz, s_xx,  u_z, s_zz^e,  s_xx^e, u_z^e определяются по формулам (2.2), (2.3), а формулы для вычисления s_xz, u_x,  s_xz^e, u_x^e имеют вид
 

sxz= 1 P+M й к л ah + ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - 1 6 Ph3e ј s щ ъ ы - ж з и he 2  +z n 1-n ц ч ш . s  ,  ux=(h-z) aP P+M + (z-h)M h(P+M) й к л ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - 1 6 Phe3 ј s щ ъ ы +           + M 2h n 1-n (h2-z2) . s - M(1-2n) 4h(1-n) (z-h)2 . s - z-h h he M 2 . s  ,

(2.5)

sxze= 1 P+M й к л ah + ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - 1 6 Ph3e ј s щ ъ ы + ж з и z3 2 + 3 4 z2he ц ч ш ј s - ж з и z + he 2 ц ч ш . s  ,  uxe=(z+he) ahP he(P+M) + (z+he)P he(P+M) й к л ж з и 2he + h 4n-1 1-n ц ч ш M 4 . s - P 6 he3 ј s щ ъ ы +           + P 12he (z+2he)(z3+he3) ј s - P 2he z(z+he) . s  .

    Деформированное состояние полосы изображено на рис. 2.

    В заключение отметим тот важный факт, что, когда на лицевых поверхностях полосы или пластины заданы нормальные перемещения, есть принципиальная разница между асимптотиками, соответствующими сжимаемому и несжимаемому материалам [3]. Когда же на лицевых поверхностях заданы другие граничные условия, то асимптотика остается одинаковой для сжимаемого и несжимаемого слоев. Для этих случаев все компоненты тензора напряжений и вектора перемещения можно вычислить по рекуррентным формулам (1.3), откуда данные несжимаемого слоя будут вытекать, если принять n = [1/2].
 

   Институт механики НАН РА
 
 

     1. Агаловян Л. А, Геворкян Р. С. -  Тр. IV Всесоюз. симпоз. по механике конструкций из композиционных материалов. Новосибирск: Наука, 1984. С. 105-110.
     2. Агаловян Л. А, Геворкян Р. С. -  ППМ. 1986. Т. 50. В. 2. С. 271-278.
     3. Агаловян Л. А, Геворкян Р. С., Саакян А. В. -  ДНАН Армении. 1997. Т. 97. № 3. С. 13-18.