ФИЗИКА
УДК 5.44
А. А. Саркисян
Диэлектрическая проницаемость электронного газа
с непараболическим законом дисперсии
(Представлено академиком Э. М. Казаряном 27/XI 1999)
При исследовании многочастичных эффектов в твердых телах принципиальным становится вопрос о выяснении роли эффектов экранирования внешнего возмущения, налагаемого на систему. К настоящему времени хорошо изучены такие эффекты, как экранирование поля примеси, эффект Кона, возникновение гало заряда вокруг поля примеси и т. д. Эти явления объясняются перераспределением носителей заряда под действием внешнего возмущающего поля. Иначе говоря, в результате решения самосогласованной задачи показывается, что реально действующий на электрон потенциал равен отношению приложенного потенциала к функции диэлектрической проницаемости ФДП
 , зависящей от длины волны и частоты приложенного возмущения.
, зависящей от длины волны и частоты приложенного возмущения.
Вместе с тем в последние десятилетия, благодаря технологическим возможностям получения низкоразмерных структур, появилось большое число теоретических и экспериментальных работ, посвященных их физическим свойствам (см. например [1,2]). Поэтому актуальным стал вопрос о вычислении ФДП таких систем. В частности, в работе [3] была вычислена ФДП размерно квантованной полупроводниковой пленки.
Закон дисперсии (ЗД) электронов при решении подобного рода задач обычно рассматривается квадратичным. Между тем в ряде случаев (например в полупроводниковых соединениях типа A3B5) ЗД электронов является непараболическим [4]. Поэтому вызывает интерес исследование эффектов экранирования в системе электронов, имеющих непараболический ЗД.
В предлагаемой работе рассмотрены эффекты экранирования в случае модели свободного электронного газа, ЗД которого совпадает по виду с релятивистским, с той лишь разницей, что роль скорости света играет некий параметр непараболичности s . Отметим, что такой выбор вида ЗД не случаен, так как, например, в двухзонном приближении для соединения InSb ЗД электрона по виду полностью совпадает с релятивистским (ЗД Кейна [4]). Роль скорости света в этом случае играет параметр взаимодействия зоны проводимости и валентной зоны s ~ 108 см/с.
В случае свободного электронного газа, находящегося под действием внешнего нестационарного возмущения, проблема нахождения Фурье-образа ФДП
 была решена Линдхардом [5]. Для
была решена Линдхардом [5]. Для
 было получено выражение
было получено выражение
|
|
|
e( |
®
q
|
, w)=1+ |
4pe2
q2
|
|
е

|
|
|
E( |
®
k
|
+ |
®
q
|
)-E( |
®
k
|
)-hw+iha |
|
, |
|
|
|
| (1) |
где
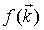 - функция распределения электронов, w и
- функция распределения электронов, w и  - соответственно частота и волновой вектор накладываемого на систему возмущения, медленно возрастающего с постоянной времени
- соответственно частота и волновой вектор накладываемого на систему возмущения, медленно возрастающего с постоянной времени - ЗД электронов, а суммирование ведется по всем состояниям |
- ЗД электронов, а суммирование ведется по всем состояниям |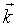 > , как заполненным, так и пустым.
> , как заполненным, так и пустым.
Пусть ЗД имеет вид
где s - параметр непараболичности, m - масса электрона. Формула Линдхарда для электронного газа с ЗД (2) в случае стационарного внешнего возмущения примет вид
|
|
|
e( |
®
q
|
, 0)=1+ |
4pe2
q2
|
|
е

|
|
|
|
Ц
|
|
h2 ( |
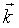 |
+ |
 |
)2s2+m2s4 |
|
- |
Ц
|
h2k2s2+m2s4
|
|
|
. |
|
|
|
| (3) |
Исследуем поведение этой функции при больших и малых значениях
 .
.
(а). При малых
 можем записать
можем записать
|
|
|
E( |
®
k
|
+ |
®
q
|
)-E( |
®
k
|
) » |
®
q
|
|
®
С
|

|
E( |
®
k
|
) |
|
|
|
| (4) |
и
|
|
|
f( |
®
k
|
)-f( |
®
k
|
+ |
®
q
|
) » - |
®
q
|
|
¶f
¶E
|
|
®
С
|

|
E( |
®
k
|
) . |
|
|
|
| (5) |
Переходя в (3) от суммирования к интегрированию, а также воспользовавшись (4), (5) и тем, что [5]
для
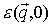 можем записать
можем записать
где l - постоянная экранирования, величина которой определяется плотностью состояний у уровня Ферми EF
где
|
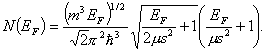 |
(9) |
Величина EF для газа с непараболическим ЗД определяется выражением
где
Учет непараболичности ЗД формально сохраняет вид 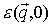 при малых значениях
при малых значениях
 (формула(7)), однако l, в отличие от электронного газа со стандартным ЗД, в этом случае имеет более сильную концентрационную зависимость, которая при EF >> ms2 переходит в l ~ n2/3, в то время как для стандартного ЗД l ~ n1/3. В частности, Фурье-образ экранированного потенциала кулоновского поля заряда, внесенного в электронный газ с непараболическим ЗД, имеет вид
(формула(7)), однако l, в отличие от электронного газа со стандартным ЗД, в этом случае имеет более сильную концентрационную зависимость, которая при EF >> ms2 переходит в l ~ n2/3, в то время как для стандартного ЗД l ~ n1/3. В частности, Фурье-образ экранированного потенциала кулоновского поля заряда, внесенного в электронный газ с непараболическим ЗД, имеет вид
где l теперь уже определяется (8) и (9), т.е. поле экранируется быстрее.
(б). При больших значениях
 постоянная экранирования l становится функцией
постоянная экранирования l становится функцией
 . Для исследования характера экранирования на малых расстояниях и при низких температурах (T® 0) необходимо в (3) перейти от суммирования к интегрированию по
. Для исследования характера экранирования на малых расстояниях и при низких температурах (T® 0) необходимо в (3) перейти от суммирования к интегрированию по
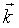 с учетом того, что функция распределения
с учетом того, что функция распределения
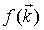 представляет собой Q-ступеньку. Результатом интегрирования является довольно громоздкое выражение, из которого, однако, можно заметить, что логарифмическая сингулярность, имеющая место в случае стандартного ЗД [5], здесь также сохраняется. Этого и следовало ожидать, поскольку для газа электронов с непараболическим ЗД поверхности Ферми сохраняют сферический вид, однако значения kF теперь уже другие.
представляет собой Q-ступеньку. Результатом интегрирования является довольно громоздкое выражение, из которого, однако, можно заметить, что логарифмическая сингулярность, имеющая место в случае стандартного ЗД [5], здесь также сохраняется. Этого и следовало ожидать, поскольку для газа электронов с непараболическим ЗД поверхности Ферми сохраняют сферический вид, однако значения kF теперь уже другие.
Выражаю благодарность Э. М. Казаряну и А. П. Джотян за плодотворное обсуждение работы.
Ереванский государственный университет
Литература
1. Казарян Э. М., Энфиаджян Р. Л. - ФТП. 1972. T. 5. C. 2002.
2. Maksym P., Chakraborty T. - Phys. Rev. Lett. 1990. V. 65. P. 108.
3. Мхоян К. А. , Саркисян А. А. - Уч. зап. ЕГУ. 1996. № 2. C. 37.
4. Цидильковский М. - Электроны и дырки в полупроводниках. М.: Наука, 1972.
5. Займан Дж. - Принципы теории твердого тела. М.: Мир, 1966.
![]() - функция распределения электронов, w и
- функция распределения электронов, w и ![]() - соответственно частота и волновой вектор накладываемого на систему возмущения, медленно возрастающего с постоянной времени
- соответственно частота и волновой вектор накладываемого на систему возмущения, медленно возрастающего с постоянной времени![]() - ЗД электронов, а суммирование ведется по всем состояниям |
- ЗД электронов, а суммирование ведется по всем состояниям |![]() > , как заполненным, так и пустым.
> , как заполненным, так и пустым. ![]() .
.![]() можем записать
можем записать
![]()
![]()
![]() можем записать
можем записать
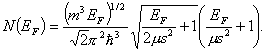
![]() при малых значениях
при малых значениях
![]() (формула(7)), однако l, в отличие от электронного газа со стандартным ЗД, в этом случае имеет более сильную концентрационную зависимость, которая при EF >> ms2 переходит в l ~ n2/3, в то время как для стандартного ЗД l ~ n1/3. В частности, Фурье-образ экранированного потенциала кулоновского поля заряда, внесенного в электронный газ с непараболическим ЗД, имеет вид
(формула(7)), однако l, в отличие от электронного газа со стандартным ЗД, в этом случае имеет более сильную концентрационную зависимость, которая при EF >> ms2 переходит в l ~ n2/3, в то время как для стандартного ЗД l ~ n1/3. В частности, Фурье-образ экранированного потенциала кулоновского поля заряда, внесенного в электронный газ с непараболическим ЗД, имеет вид
![]() постоянная экранирования l становится функцией
постоянная экранирования l становится функцией
![]() . Для исследования характера экранирования на малых расстояниях и при низких температурах (T® 0) необходимо в (3) перейти от суммирования к интегрированию по
. Для исследования характера экранирования на малых расстояниях и при низких температурах (T® 0) необходимо в (3) перейти от суммирования к интегрированию по
![]() с учетом того, что функция распределения
с учетом того, что функция распределения
![]() представляет собой Q-ступеньку. Результатом интегрирования является довольно громоздкое выражение, из которого, однако, можно заметить, что логарифмическая сингулярность, имеющая место в случае стандартного ЗД [5], здесь также сохраняется. Этого и следовало ожидать, поскольку для газа электронов с непараболическим ЗД поверхности Ферми сохраняют сферический вид, однако значения kF теперь уже другие.
представляет собой Q-ступеньку. Результатом интегрирования является довольно громоздкое выражение, из которого, однако, можно заметить, что логарифмическая сингулярность, имеющая место в случае стандартного ЗД [5], здесь также сохраняется. Этого и следовало ожидать, поскольку для газа электронов с непараболическим ЗД поверхности Ферми сохраняют сферический вид, однако значения kF теперь уже другие.