УДК 621.38
Модель формирования пористой матрицы
(Представлено 18/XI 1999)
1. Введение. Неспадающий интерес к люминесценции и другим оптическим явлениям в пористом кремнии (ПК)[1] требует дальнейших исследований, направленных на понимание физических процессов, протекающих в нем. Неординарные свойства этого материала, несомненно, связаны с его нерегулярной геометрической структурой, образующейся, например, в процессе анодного растворения монокристаллического кремния (c-Si) во фтористой среде
(HF (50%) : H2O : C2H5OH = 1 :1 : 2) и изменяющейся от образца к образцу [2-4]. В результате такого неконтролируемого процесса порообразования формируется пористая матрица, важнейшие параметры которой (например, значение пористости, размер микрокристаллитов и пор) предопределяются значением тока, протекающего через систему, временем процесса электрохимического травления, типом проводимости c-Si и т.д.
Нами в работе [5] была предложена фрактальная модель для описания сложной структуры ПК. В ней предполагалось появление на поверхности Nk=nk пор (полусферических, конусообразных или цилиндрических) с радиусом
| (1) |
где r0 - размер первой (наибольшей) поры, n,m > 1 - параметры распределения пор, которые определяют фрактальную размерность поверхности как DF=logmbn, b > 1 - параметр "обратной связи", обуслoвливающий увеличение радиусов пор с индексом k-1 в b раз при появлении на поверхности материала пор с радиусом rk.
Такое распределение позволяет вычислить некоторые важные параметры пористой
матрицы, в частности, увеличение площади поверхности S и значение пористости p
материала, средний размер пор `r и среднее расстояние между ними, зависящие от значения фрактальной размерности DF. Было установлено, в частности, что площадь пористой поверхности линейно растет с увеличением значения его пористости и при определенных параметрах может увеличиться в 2, 2.5 и 3.2 раза для полусферических, конусообразных и цилиндрических (с радиусом основания, равным высоте цилиндра) пор, соответственно.
В настоящей работе сделана попытка дальнейшего развития вышеизложенной модели с целью описания более реального процесса порообразования, включающего в себя развитие во времени пористой поверхности и зависимости его параметров от значения тока анодизации.
2. Модель временного развития пор. Предположим, что в процессе электрохимического травления на гладкой поверхности материала через равные промежутки времени t1 появляется nk пор с радиусом
| (2) |
где v - скорость увеличения первой поры (k=0) по направлению параллельной поверхности материала (скорость травления), t - время.
|
|
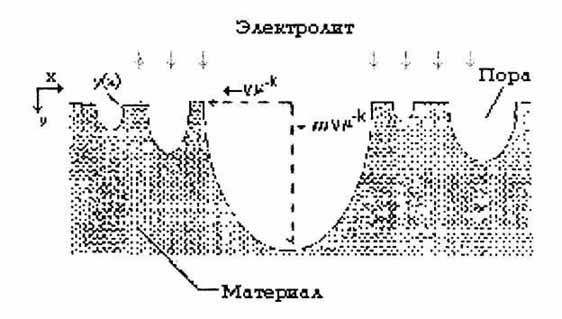
Рис. 1. К описанию модели порообразования.
Фрактальная размерность в этом случае определяется как DF=logmbn. Пусть для общности рассмотрения поры имеют форму полуэллипсоидов (см. рис.1), полуоси которых растут со скоростью vm-k и mvm-k по направлениям параллельной и перпендикулярной поверхности, соответственно. Отметим, что нетрудно провести конкретные расчеты параметров пористой матрицы для случаев конусообразных и цилиндрических пор. Однако так как эллипсоид имеет промежуточную между конусом и цилиндром форму поверхности, то проведем расчеты лишь для вышеуказанного случая. Кроме того, при U-образной технологии для диэлектрической изоляции образующиеся поры более похожи на эллипсоиды, чем на точные цилиндры.
Ясно, что численный коэффициент m и постоянная времени t1 зависят от различных физических параметров полупроводникового материала (например, степени легирования, кристаллографической ориентации), тока анодизации, температуры и состава электролита и т. д. Конкретные зависимости m и t1 от этих параметров в настоящей работе не обсуждаются.
2.1 Пористая поверхность. При предложенном профиле пор нетрудно вычислить площадь образовавшейся пористой поверхности, которая равна
| (3) |
где S0 - первоначальная площадь поверхности (без пор), S - площадь образовавшейся поверхности, Sос - суммарная площадь оснований всех пор (т. е. сумма площадей всех кругов на поверхности), Sбок - суммарная площадь боковой поверхности пор.
Последнюю можно вычислить следующим образом: площадь поверхности, образующаяся при вращении полуэллипса y(x) вокруг оси y, определяется формулой
| (4) |
где a - полуось по направлению x. Так как в нашем случае имеем дело с полуэллипсом [(x2)/(a2)]+[(y2)/((ma)2)]=1 со значением m, большим единицы (рис.1), то вычисление интеграла (4) показывает, что площадь этой поверхности в
|
|
(5) |
раз больше площади основания образовавшегося полуэллипсоида pa2.
Принимая во внимание, что в соответствии с нашей моделью для каждой поры с индексом k полуось a равна vm-k(t-kt1), можно определить суммарные площади оснований Sос и боковых поверхностей Sбок всех пор в момент времени t по формулам
| (6) |
|
Sбок=q·Sос. |
(7) |
После вычисления конечного ряда (6) для площади образовавшейся поверхности в момент времени t получим следующее выражение:
|
|
(8) |
Для проведения дальнейших численных расчетов допустим, что первоначальная поверхность имеет форму круга радиусом R.
Пористость поверхности pS определяется как соотношение суммарной площади оснований всех пор Sос и первоначальной площади S0 и равна
|
|
(9) |
Из анализа выражений (8) и (9) очевидно, что площадь образовавшейся поверхности и значение его пористости, являющиеся функциями от времени, зависят также от других параметров материала и электрохимической системы, таких, как время t1, необходимое для появления нового поколения пор, степень шероховатости поверхности DF, параметры распределения пор n, m, связанные друг с другом через DF, скорость увеличения размеров пор по поверхности v. Параметр t1 в свою очередь должен зависеть как от плотности тока j системы, температуры и состава электролита, так и от степени идеальности поверхности исходного травящегося материала и его физических параметров.
Следует отметить, что соотношение осей эллипса (скоростей травления в перпендикулярной и параллельной поверхности материала направлениях) m присутствует только в выражении для площади пористой поверхности (через q) и, естественно, никоим образом не влияет на значение поверхностной пористости.
На рис. 2 приведена зависимость относительного увеличения площади поверхности материала S(t)/S0 от времени при различных значениях m и параметрах DF=2.5, v=5·10-4 см/с, t1=4 с.
В рамках нашей модели слиянием пор пренебрегается, а на эксперименте, где неизбежным образом имеет место слияние меньших пор с большими, естественно, наблюдается меньшее число пор, чем реально было образовано в процессе электрохимического травления. Это означает, что
наша модель имеет ограничение во времени. Графический анализ также показывает, что увеличение площади S(t) сильно зависит от соотношения между скоростями травления параллельно и перпендикулярно поверхности (параметра m) и, соответственно, выбором кристаллографической ориентации (c-Si).
|
|
Рис. 2. Зависимость относительного увеличения площади пористой поверхности для
исходной единичной площади S0=1 см2 при значениях m=2,3,4,5.
|
|
а) б)
Рис. 3. Зависимости знaчения пористости от времени порообразования (а) и
относительного увеличения площади поверхности (б).
На рис. 3, а представлена временная зависимость значения пористости p(t) при параметрах n = 5·10-4 см/с, t1=4 с и различных значений фрактальной размерности DF. Из рисунка ясно, что чем грубее поверхность материала (больше DF), тем быстрее растет значение пористости.
Из сравнения выражений (8) и (9) следует ожидаемое из общих соображений соотношение между значениями относительного увеличения площади образовавшейся поверхности и его пористости:
| (10) |
т.е. площадь пористой поверхности линейно растет со значением пористости (рис. 3, б).
2.2. Пористый объем. Значение пористости, определяемое экспериментально в основном весьма грубым пикнометрическим методом (взвешиванием материала до и после электрохимической реакции), соответствует доле воздушных пор в материале, т.е. доле суммарного объема всех пор.
С помощью модели, предложенной в настоящей статье, нетрудно вычислить значение объемной пористости материала, которая должна определяться как соотношение объемов всех пор и пористой матрицы. Такое определение для пористости справедливо лишь в случае, когда еще не разрушен приповерхностный слой (см. рис. 1), т. е. значение пористости на плоскости x=0 не достигло значения pS=1. Для получения соответствующего выражения необходимо вначале вычислить суммарный объем пор V(t) по следующей формуле:
| (11) |
Эта сумма также сходится, и для суммарного объема пор получается весьма сложное выражение. Так как объем пористой матрицы V0 равен pr2v t, то для значения объемной пористости pv получим
|
| (12) |
Сразу же отметим, что объемная пористость, в отличие от поверхностной, линейно зависит от параметра m и, аналогично поверхностной пористости, является квадратичной функцией скорости увеличения размеров пор v. На рис. 4 приведены кривые, вычисленные по формуле (12) для различных значений m, а также соответствующая зависимость значения поверхностной пористости.
Перейдем к обсуждению вопроса о влиянии значений тока анодизации на разные параметры образовавшейся пористой матрицы, в частности, на значение пористости материала.
Расчеты, проведенные В. Лехманом в [7], приводят к корневым зависимостям радиуса и глубины макропор от тока в электрохимической системе, что и было обнаружено экспериментально в той же работе. Если сделать предположение, что радиус поры линейно растет со временем, то для скорости увеличения размера пор можно написать
| (13) |
Есть и другие работы (см., например, рис. 10 в работе [8]), в которых экспериментально наблюдалась корневая зависимость скорости фронта травления от тока анодизации. Эту скорость можно определить как среднее арифметическое от всех скоростей увеличения глубин пор.
Учитывая соотношение (13), из выражений для значений поверхностной и объемной пористостей, полученных в пунктах 2.1 и 2.2 настоящей работы, вытекают следующие соотношения:
| (14.1,2) |
Существуют экспериментальные данные о наблюдавшейся линейной зависимости между значением пористости материала и током электрохимической системы [9]. Из соотношений (14.1) и (10) вытекает также, что значение площади образовавшейся поверхности S линейно растет с увеличением тока анодизации.
Теоретическое определение коэффициентов пропорциональности в выражениях (14.1,2) является весьма трудной задачей, при решении которой должно учитываться большое количество параметров электрохимической системы.
|
|
Рис. 4. Временная зависимость объемной пористости pv при значениях m=5,8,10,15.
Заключение. Фрактальная модель пористого материала, развития в настоящей работе, открывает новую возможность моделирования сложного процесса порообразования.
Путем введения в рассмотрение временной зависимости увеличения размеров пор вычислены тaкие важные параметры пористой матрицы, как площадь образовавшейся поверхности, значение поверхностной и объемной пористости. Показано, в частности, что площадь образовавшейся поверхности сильно зависит от разности между скоростями увеличения размеров пор в направлениях параллельно и перпендикулярно поверхности материала и, тем самым, кристаллографической ориентации кремния. Например, при соотношении m=5 площадь первоначальной поверхности может увеличиться в 50 раз еще при значении пористости поверхности всего 60%.
Значение пористости (как поверхностной, так и объемной), а также площадь образовавшейся пористой поверхности линейно зависят от тока анодизации. Эти результаты находятся в соответствии с другими теоретическими [8] и экспериментальными данными [9].
Данная работа выполнена в рамках темы 96-907, финансируемой Министерством образования и науки РА и субконтракта IPP-AAX-8-17660-01.
Ереванский государственный университет
Литература
1. Canham L.T. - Appl. Phys. Lett. 1990. V. 57. P. 1046.
2. Cullis A.G., Canham L.T. - Nature. 1991. V. 333. P. 335
3. Smith R.L., Collins S.D. - J. Appl. Phys. 1992. V. 71. P. R1-R22.
4. Lin Ch.-H. et al., - J. Appl. Phys. 1992. V. 75. P. 7728-7736
5. Арутюнян В.М., Гулинян М.Ж., Трибуч Г. - Мат. II нац. конф., Дилижан. 1999. С. 20-23.
6. Léacute etant S., Vial J.C. - J. Appl. Phys. 1997. V. 82. P. 397
7. Lehman V. - Thin Solid Films. 1995. V. 255. P. 1-4
8. Theib W. - Surface Science Reports. 1997. V. 29. P. 91-192
9. Fronhoff S. et al - Thin Solid Films. 1995. V. 255. P. 59-62