где B и L-барионный и лептонный заряды частиц. Эта формула применима и для кварков, для которых B=1/3 и L=0. Таким образом, закон сохранения B-L в работе [2] получен как следствие SU(5) симметрии, а в работе [1] - как следствие закона сохранения s-числа. Из сохранения s-числа, в частности, следует, что, в согласии с теорией Дирака-Вейля и SU(5) симметрией [3,4], масса электронного нейтрино в точности равна нулю.
    В другой работе авторов [5], исходя из распределения кварков и лептонов на плоскости (q, s) , была выявлена природа кварк-лептонной симметрии. В частности, было показано, что для частиц одного поколения существует группа преобразования симметрии, представляемая 4-группой диэдра [6].
    Естественно ожидать, что существует симметрия также и между всеми бесцветными частицами. При этом, кроме лептонов и мезонов, мы имеем в виду все барионы, которые в принципе могут быть составлены из восемнадцати известных кварков (индекс указывает на цвет):

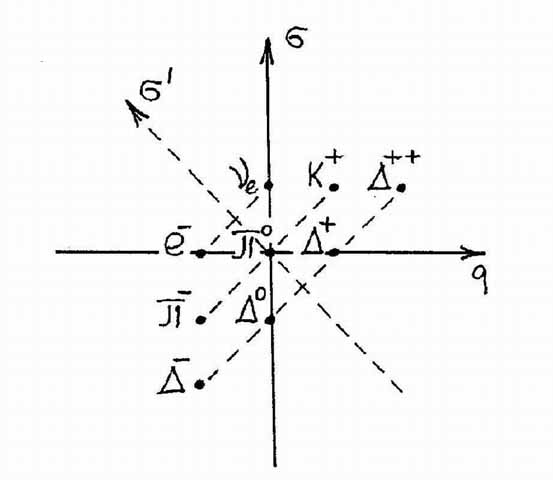
    В пользу такой возможности говорят как простая кварковая структура барионов, так и распределение обычных частиц на плоскости (q , s). При этом в каждой отмеченной точке мы поместили по одной частице в качестве представителя нескольких частиц (см. рис. 1). Например, в точке (-1,0), кроме электрона, надо подразумевать и остальные заряженные лептоны m^- и t^-. Из рисунка видно, что имеет место симметрия по отношению к оси s ў. При этом число частиц в симметричных точках одинаково. Легко показать, что такая симметрия имеет место также и для многокварковых барионов. Например, если барионы с квантовыми числами B=5,   q=3,    s=-2 состоят из восьми верхних и семи нижних кварков, то симметрично расположенные барионы B=5,   q=3,    s=-3 , наоборот, состоят из семи верхних и восьми нижних кварков. Очевидно, что число бесцветных комбинаций одинаково.

Рис. 1. Распределение обычных частиц на плоскости (q, s). За единицу
измерения принято расстояние между соседними узлами по обеим осям.

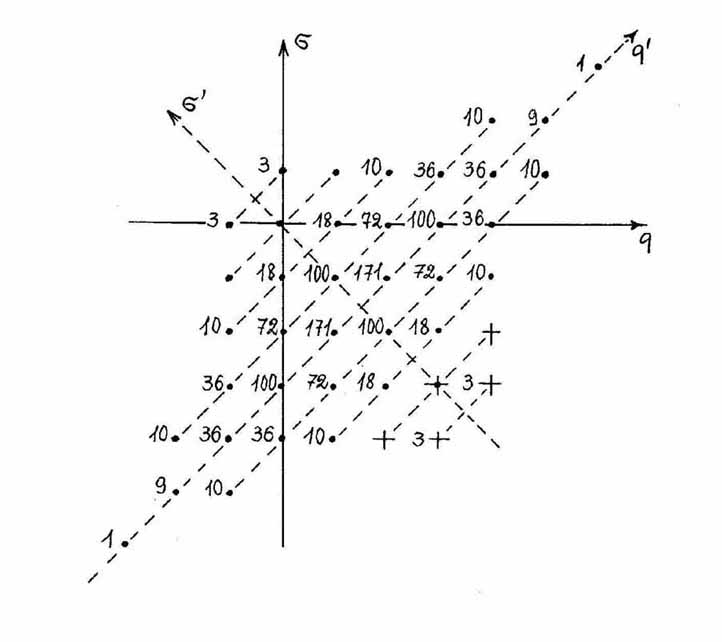
    Для барионов аналогичная симметрия имеет место также и по отношению к другой оси qў, определяемой уравнением s=q-3 . Легче всего в этом убедиться прямым подсчетом числа частиц во всех отмеченных точках (рис. 2). Числа, приведенные на рисунке, указывают на число возможных частиц в данном узле. Пунктирные линии, параллельные оси qў, удовлетворяют уравнениям s=q-B. При этом вместо лептонного числа мы приписываем барионное число B=-1 лептонам, так как разность B-L сводится к числу B для барионов и к числу L для лептонов. Тогда вместо закона сохранения B-L можно говорить о законе сохранения барионного числа. Это, на первый взгляд, формальное переименование может привести, однако, к интересным физическим последствиям. Отсюда, в частности, следует, что во всех реакциях, где участвуют антипротоны, их можно заменить на электрон с добавкой необходимой энергии. С тем же основанием протон можно заменить на соответствующий позитрон.

Рис. 2. Распределение всех бесцветных частиц на плоскости (q, s).
В узлах, отмеченных крестиками, находятся трансбарионные частицы.
Числа у узлов указывают на число возможных частиц в данном узле.

    После замены лептонного заряда на барионный заряд формулу (2) можно заменить формулой s=q-B. На прямой, определяемой этим уравнением, находятся все частицы с барионным числом B. В точке (q=3,  s=-3,  B=6) имеется лишь одна частица, состоящая из всех восемнадцати кварков.
    Распределение частиц на рис. 2 подсказывает, что для завершения картины наблюдаемой симметрии необходимо в отмеченных крестиками точках подразумевать наличие некоторых новых частиц. Например, в точке (q=4,  s=-3) должны существовать три частицы, так как в симметричной с ними точке имеется три лептона. После этого распределение всех бесцветных частиц будет подчиняться той же группе преобразования подобий, которой подчиняются частицы одного поколения [5]. Предсказанные частицы находятся в пяти узлах, расположенных симметричным образом по отношению к лептонам и мезонам. Эти частицы, как и лептоны, не имеют кварковой структуры, так как для них B=6 и B=7. Надо полагать, что эти частицы (назовем их трансбарионными) на порядок тяжелее обычных тяжелых барионов.
    Если в некотором узле, по каким-то правилам отбора, будет отсутствовать некоторое число частиц или даже все возможные частицы, то вследствие симметрии такое же число частиц должно отсутствовать и в остальных симметричных с ними узлах. Это замечание к отмеченным нами трансбарионным частицам не относится, так как симметричные с ними лептоны и мезоны уже давно известны. Отметим, что симметрия имеет место вне зависимости от числа поколения. К сожалению, это обстоятельство не дает нам возможности судить о наличии четвертого поколения. Однако обнаружение хотя бы одной частицы из сотни возможных частиц, находящихся за пределами третьего поколения, будет свидетельствовать о наличии четвертого поколения. Такими могут оказаться, например, частицы с B=4 и q=±2, ±3, ±4. Другим свидетельством может служить наличие в одном узле большего числа частиц, чем это допустимо в пределах трех поколений. Например, если будет обнаружено более одной частицы с зарядами q=6,  B=3 или q=-3,  B=3. При наличии четвертого поколения число таких частиц может достигнуть двадцати.
    В заключение отметим, что существование трансбарионных частиц также не зависит от числа поколений.

    Армянский педагогический институт им. Абовяна

    1. Корхмазян Н. А.- ДНАН Армении. 1999. Т. 99. N 2. С. 182-185.
    2. Georgi H., Glashow Sh.- Phys. Rev. Lett. 1974. V. 32. N 8. P. 438.
    3. Окунь Л. Б. Физика элементарных частиц. М.: Наука, 1987.
    4. Хелзен Ф., Мартин А. Кварки и лептоны. М.: Мир, 1987.
    5. Корхмазян Н. А., Корхмазян Н. Н.- ДНАН Армении. 1999. Т. 99. N 4. С. 347-350.
    6. Вигнер Е. Теория поля. М.: ИЛ, 1961.