МЕХАНИКА
УДК 239.374
Г. В. Геворкян
Прочность плиты при концентрации напряжений
(Представлено академиком М. А. Задояном 9/II 2000)
Теоретические исследования прочности тела при различных условиях сводятся к решению задачи о состоянии тела с точки зрения малонапряженности или концентрации напряжений в угловой точке. Если тело не имеет концентрационных точек или концентраторов, то вопрос ограничивается обычным классическим методом вычисления границ прочности тела (материала). Однако особый интерес представляет состояние концентрации напряжений - ведь в реальных условиях в большинстве случаев технически невозможно избежать этого состояния. Возникает вопрос о вкладе концентрации напряжений в уменьшение запаса прочности тела, а также о зависимости его от геометрических и механических параметров концентратора. Есть некоторые работы в этом направлении [1-3]. Настоящая работа тоже выполнена для нахождения ответа на вышеуказанные вопросы, но только для частного случая - изгиба однородной плиты с концентратором. Для расчетов используется широко известный в строительной механике метод сечений [1].
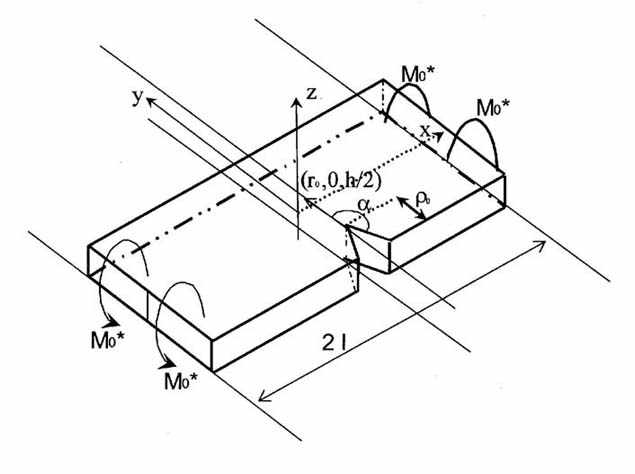
Пусть однородная плита с поперечным угловым вырезом (со входящей угловой выточкой, в частности со щелью) подвергается поперечному изгибу (рис. 1). Допускается степенной закон упрочнения материала s0=ke0m .
Согласно методу сечений нужно иметь решение в целом для изгиба такой плиты без входящей выточки, а также местное решение окрестности угловой точки выточки плиты [1,3]. Для решения первой задачи, т. е. решения в целом, берутся декартова система координат и классические приближения.
|
|
|
Рис. 1. Прочность плиты при концентрации напряжений. |
Для изгибающих моментов имеем:
Изгибающие моменты выражаются через напряжения
|
|
|
sij(x, y, z)= |
Mij(x, y)
2I
|
z/z/m-1 , |
|
|
|
|
где h - толщина плиты и I= [1/(m+2)] ( [h/2] ) m+2 .
Из системы уравнений равновесия получаем
|
|
|
|
¶2Mx
¶x2
|
+2 |
¶2Mxy
¶x¶y
|
+ |
¶2My
¶y2
|
=0 .
|
|
|
|
| (3) |
Устанавливая выражения (1) для моментов в (3), получим
|
|
|
|
¶2
¶x2
|
|
й
к
л
|
k0m-1 |
ж
з
и
|
kx+ |
1
2
|
ky |
ц
ч
ш
|
щ
ъ
ы
|
+2 |
¶2
¶x ¶y
|
[k0m-1 kxy]+ |
¶2
¶y2
|
|
й
к
л
|
k0m-1 |
ж
з
и
|
ky+ |
1
2
|
kx |
ц
ч
ш
|
щ
ъ
ы
|
=0 .
|
|
|
|
| (4) |
Учитывая, что ky=0; kxy=0; k0= | kx | и не зависят от y , т. е. перемещение w=w(x) , уравнение (4) примет следующую форму:
|
|
|
|
d2
dx2
|
[ | kx | m-1kx ]=0 .
|
|
|
|
| (5) |
Решением этого уравнения является:
Учитывая следующие граничные условия:
|
|
|
Mx | x=±l=D | kx | m-1kx | x=±l=M0 и wx | x=±l=0 ,
|
|
|
|
|
получим для номинального решения соответственно следующие выражения:
|
|
|
|
sx= |
M0
2I
|
z | z | m-1 , sy= |
M0
4I
|
z | z | m-1 ,
|
|
|
w= |
1
2
|
|
ж
з
и
|
|
M0
D
|
ц
ч
ш
|
[1/m]
|
(l2-x2) .
|
|
|
|
| (7) |
А теперь рассмотрим местное решение согласно [4], полученное в цилиндрической системе (r, q, z) координат.
Согласно нашей задаче материал несжимаем и упрочняем по степенному закону:
|
|
|
|
Ç
s0
|
=k |
Ç
e0m
|
, |
Ç
er
|
+ |
Ç
eJ
|
+ |
Ç
ez
|
=0 . |
|
|
|
|
Для местного решения используется уточненная теория. Компоненты моментов будут:
|
|
|
|
Ç
Mr
|
=Ak |
Ç
I
|
r(l-1)m |
й
к
л
|
|
ж
з
и
|
|
l
2
|
+1 |
ц
ч
ш
|
j+ |
1
2
|
fў |
щ
ъ
ы
|
c ,
|
|
|
|
Ç
MJ
|
=Ak |
Ç
I
|
r(l-1)m |
й
к
л
|
|
ж
з
и
|
|
l
2
|
+1 |
ц
ч
ш
|
j+fў |
щ
ъ
ы
|
c ,
|
|
|
|
Ç
MrJ
|
=A |
1
4
|
k |
Ç
I
|
r(l-1)m[ fў+( l-1 ) f] c ,
|
|
|
|
Ç
Qr
|
=Ak |
Ç
J
|
r(l-1)m+1[ f+( l+1 ) f ] c ,
|
|
|
|
Ç
QJ
|
=Ak |
Ç
J
|
r(l-1)m+1[ fў+f] c ,
|
|
|
|
| (8) |
где c = ( Ц{jў2+(l+2 ) jfў+( l2+l+1 ) j2+[1/4] [ jў+( l-1 ) f]2} )m-1, j и f есть функции напряжений, а A неопределенная постоянная (коэффициент) [4].
При малых r , т. е. для малой окрестности нашей угловой точки, имеем
|
|
|
|
Ç
I
|
» |
hm+2
m+2
|
, |
Ç
J
|
» |
hm
m
|
. |
|
|
|
|
|
|
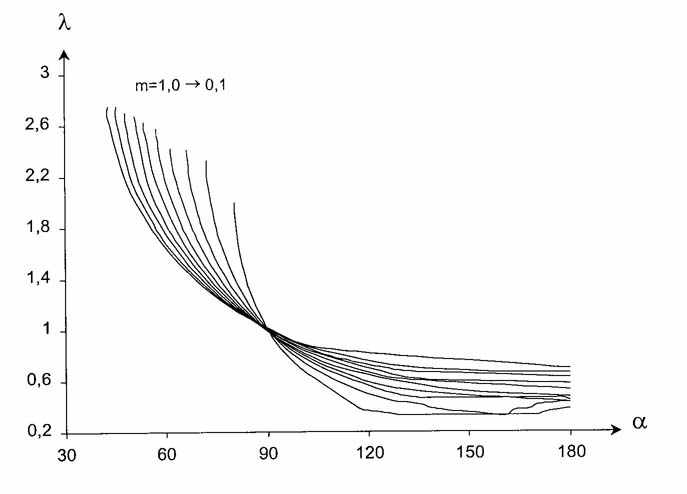
Рис. 2. Графики зависимости l
от угла выточки (2p-2a) при разных
m.
Графики получены путем решения системы дифференциальных
уравнений
второго порядка из [4] численным
методом.
На рис. 2 изображены графики зависимости l от угла выточки при разных m, полученные путем решения системы дифференциальных уравнений второго порядка из [4] численным методом.
Имея номинальное (7) и местное (8) решения, согласно методу сечений получим
|
|
|
|
Ç
MJ
|
(r0 , 0)=Mx ( x | x=a , y | y=r0+r )=M0 ,
|
|
|
|
ro
у
х
0
|
|
Ç
MJ
|
(r , 0) dr= |
rо+ro
у
х
0
|
Mx(a, y) dy = M0 ·(r0+r0) .
|
|
|
|
| (9) |
Подставляя выражения местных решений (8) в (9) , получим
|
|
|
r0=r0 |
ж
з
и
|
|
1
(1-l)m
|
-1 |
ц
ч
ш
|
,
|
|
|
Ak |
Ç
I
|
= |
M0
|
|
й
к
л
|
|
ж
з
и
|
|
l
2
|
+1 |
ц
ч
ш
|
j(0 , l)+fў(0 , l) |
щ
ъ
ы
|
c(0 , l) |
|
|
й
к
л
|
r0 |
ж
з
и
|
|
1
(1-l)m
|
-1 |
ц
ч
ш
|
щ
ъ
ы
|
(1-l)m
|
,
|
|
|
|
| (10) |
Выражения для [ \frown || (Mq )] (r , J) напишем в следующих выражениях:
|
|
|
|
Ç
Mq
|
(r , J)= |
M0
|
|
й
к
л
|
r0 |
ж
з
и
|
|
1
(1-l)m
|
-1 |
ц
ч
ш
|
щ
ъ
ы
|
(l-1)m
|
|
r(l-1)m ×
|
|
|
× |
|
|
й
к
л
|
|
ж
з
и
|
|
l
2
|
+1 |
ц
ч
ш
|
j (J, l) +fў(J, l) |
щ
ъ
ы
|
c(J, l) |
|
|
й
к
л
|
|
ж
з
и
|
|
l
2
|
+1 |
ц
ч
ш
|
j (0, l) +fў(0, l) |
щ
ъ
ы
|
c(0, l) |
|
.
|
|
|
|
| (11) |
После введения обозначений
|
|
|
N= |
M0
|
|
й
к
л
|
r0 |
ж
з
и
|
|
1
(1-l)m
|
-1 |
ц
ч
ш
|
щ
ъ
ы
|
(l-1)m
|
|
|
|
|
|
| (12) |
перепишем выражения (11) в форме
|
|
|
|
Ç
Mq
|
(r , J)=Nr(l-1)mF(J) , |
|
|
|
| (13) |
где
F(q)= [([ ( [(l)/2] +1 ) j (J, l) +fў(J, l) ] c(J, l))/([ ( [(l)/2] +1 ) j (0, l) +fў(0, l) ] c(0, l))]
.
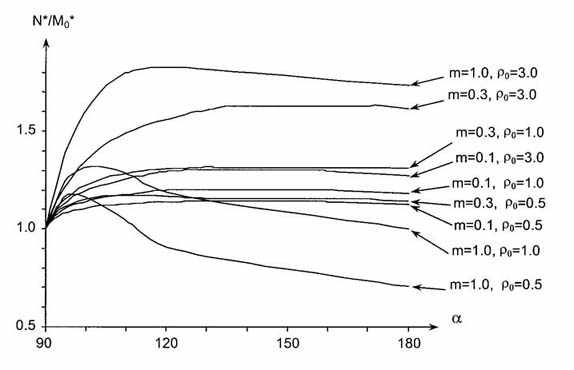
Из (13) видно, что N есть аналог коэффициента интенсивности напряжений из [1,3]. Поэтому назовем N коэффициентом интенсивности моментов. На рис. 3 изображены графики зависимости соотношения коэффициента интенсивности и разрушающего номинального момента (обозначен звездочкой) от угла выточки из формулы (12) при разных глубинах выточки и m .
|
|
Рис. 3. Зависимость соотношения коэффициента
интенсивности
и разрушающего номинального момента от угла
выточки.
Для местных разрушающих моментов (обозначены звездочкой) в окрестности угловой точки на линии x=0 или же J = 0 из (12) получим
|
|
|
|
Ç
M
|
*
q
|
(r , 0)= |
M0*
|
|
й
к
л
|
|
1
(1-l)m
|
-1 |
щ
ъ
ы
|
(l-1)m
|
|
|
ж
з
и
|
|
r
ro
|
ц
ч
ш
|
(l-1)m
|
.
|
|
|
|
| (14) |
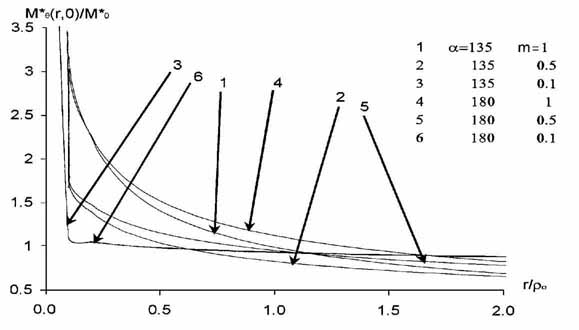
Из формулы (14) видно, как будут вести себя значения моментов по мере приближения к концентрационной точке по линии y=a. На рис. 4 изображены графики зависимости соотношения местного разрушающего момента на линии J=0 и номинального разрушающего момента от соотношения расстояний от концентратора и глубины выточки при ее разных углах и m.
Из вышеприведенных формул видно, что экспериментально можно получить значения l, которые зависят от угла входящей выточки и которые можно сверить с теоретическими расчетами.
|
|
Рис. 4. Зависимость соотношения местного разрушающего
момента
на линии J=0 и номинального
разрушающего момента от соотношения
расстояния от концентратора и глубины выточки при ее
разных углах и m.
Автор благодарит М. А. Задояна за обсуждения и ценные замечания об этой работе.
Институт механики НАН РА
Литература
1. Партон В. З., Морозов В. М. Механика упругопластического разрушения. М.: Наука, 1992.
2. Справочник по коэффициентам интенсивности напряжений. Т. 1-2. Под ред. Ю. Мураками. М.: Мир, 1990.
3. Задоян М. А.- ПМТФ. 1997. Т. 38, N 6.
4. Задоян М. А.- ДНАН Армении. 1998. Т. 98, N 4. С. 269-273.



